Solution pour le challenge 15
On observe que, pour tout ![]() :
:
![]()
L’équation caractéristique pour l’équation homogène est ![]() et ses solutions sont -1 et 1.
et ses solutions sont -1 et 1.
Une suite particulière vérifiant
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{ccc}\frac{3}{2}+\lambda-\mu & = & 1\\\\3+\lambda+\mu & = & 2\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bfa1192ca4441ca2f31177dca5e5835a_l3.png)
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{ccc}\lambda & = & -\frac{3}{4}\\\\\mu & = & -\frac{1}{4}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b326f87ae7780f7fe05541a9055e7aa6_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{u_{n}=\frac{6n-3-\left(-1\right)^{n}}{4}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8eb8b2ecbaa9e05f2a36c163907db4f3_l3.png)
On peut dire que la formule ci-dessus n’était pas évidente à conjecturer, sur la base des quelques premiers termes de la suite !
On calcule alors :
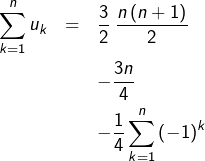
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^{n}u_{k}=\frac{6n^{2}+1-\left(-1\right)^{n}}{8}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-161eb739609a0eda7ea70ec477bbf7fb_l3.png)
Pour consulter l’énoncé, c’est ici

