Lettre Q

QUANTIFICATEUR

En mathématiques, on utilise de façon permanente les symboles :

  • d’égalité =
  • d’appartenance ∈
  • d’inclusion ⊂
  • d’implication ⇒
  • d’équivalence logique ⇔

A ceux-là s’ajoutent \forall et \exists qu’on appelle les quantificateurs.

Quantificateur Existentiel →

← Quantificateur Universel

Exemple 1

L’assertion

    \[\forall x\in\mathbb{R},\thinspace x^{2}\geqslant0\]

signifie que pour tout nombre réel x, le carré de x est positif ou nul.

Elle est vraie, c’est bien connu 🙂

Exemple 2

L’assertion

    \[\exists y\in\mathbb{R};\thinspace\forall x\in\mathbb{R},\thinspace y\geqslant x\]

signifie qu’il existe un réel plus grand que tous les autres.

Elle est bien entendu fausse …

Lorsque deux quantificateurs distincts se suivent, l’ordre importe !

Ainsi, dans l’exemple ci-dessus, on obtient après interversion la nouvelle assertion :

    \[\forall x\in\mathbb{R},\,\exists y\in\mathbb{R};\,y\geqslant x\]

et celle-ci est vraie car, pour tout réel x, on peut trouver un réel y plus grand que x … par exemple : y=x+1.

Pour en savoir davantage sur l’interversion de quantificateurs, voir cet article.

Exemple 3

L’assertion

    \[\exists a\in\left\llbracket 0,96\right\rrbracket ;\thinspace a^{2}\equiv-1\pmod{97}\]

signifie qu’il existe un entier compris (au sens large) entre 0 et 96, dont le carré est congru à -1 modulo 97.

En effet :

    \[22^{2}=484=4\times97+96\equiv-1\pmod{97}\]

Mais cet entier n’est pas unique, puisque

    \[75^{2}=5625=57\times97+96\equiv-1\pmod{97}\]

Exemple 4

Pour exprimer l’existence et l’unicité d’un objet possédant une propriété donnée, on place un point d’exclamation juste après le quantificateur existentiel. Ainsi, l’assertion :

    \[\forall y\in\mathbb{R},\thinspace\exists\textbf{ ! }x\in\mathbb{R};\thinspace x+e^{x}=y\]

signifie que tout réel y peut s’écrire sous la forme x+e^{x} pour un unique réel x.

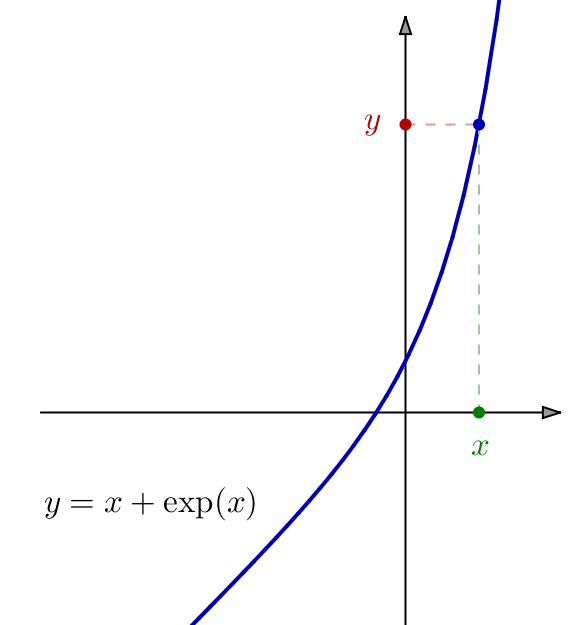
Elle exprime donc le caractère bijectif de l’application \mathbb{R}\rightarrow\mathbb{R},\thinspace x\mapsto x+e^{x}.

Exemple 5

L’assertion

    \[\forall n\in\mathbb{N}-\{0,1\},\thinspace\exists\left(p,q\right)\in\mathbb{P}^{2};\thinspace p+q=2n\]

signifie que tout nombre entier pair supérieur ou égal à 4 est la somme de deux nombres premiers.

Nul ne sait, à ce jour (février 2021), si elle est vraie… c’est la célèbre conjecture de Goldbach.

Partager cet article