Toutes les vidéos en FRANÇAIS sont accessibles depuis cette page.
Toutefois un projet de vidéos en ANGLAIS est en cours de développement et vous pouvez y accéder en cliquant ici
VIDÉOS RÉCENTES EN TÊTE …
La formule ![]() donnant la valeur de l’intégrale de Gauss est très célèbre. Cette vidéo en propose quatre démonstrations. C’est l’occasion d’une belle promenade dans l’univers tellement riche du calcul intégral !
donnant la valeur de l’intégrale de Gauss est très célèbre. Cette vidéo en propose quatre démonstrations. C’est l’occasion d’une belle promenade dans l’univers tellement riche du calcul intégral !
En notant ![]() , il est classique que
, il est classique que ![]() pour tout ENTIER
pour tout ENTIER ![]() . On prouve dans cette vidéo, en utilisant les fonctions
. On prouve dans cette vidéo, en utilisant les fonctions ![]() et
et ![]() d’Euler, que l’égalité reste vraie pour tout RÉEL
d’Euler, que l’égalité reste vraie pour tout RÉEL ![]() .
.
Une présentation élémentaire de la célèbre inégalité de Cauchy-Schwarz, suivie de cinq petits exercices d’application, dans des domaines variées : géométrie, olympiades, combinatoire, probabilités et calcul intégral.
L’un de mes étudiants m’a demandé, il y a de cela quelques années, s’il était possible de calculer de manière exacte la fraction continue 1 + 2 / (3 + 4 / (5 + …))
Cette vidéo propose une réponse détaillée.
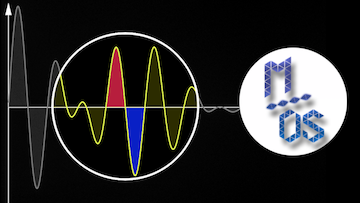
Un exercice classique consiste à prouver que l’application ![]() est continue sur
est continue sur ![]() et dérivable sur
et dérivable sur ![]() . Dans cette vidéo, on montre notamment sa NON dérivabilité en 0.
. Dans cette vidéo, on montre notamment sa NON dérivabilité en 0.
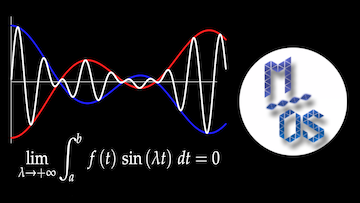
Cette vidéo constitue une suite de la précédente. On y donne une preuve du lemme de Riemann – Lebesgue qui suit de près l’intuition géométrique : les aires de deux arches consécutives se compensent presque et cette compensation persiste globalement.
Si ![]() est continue par morceaux, alors l’intégrale
est continue par morceaux, alors l’intégrale ![]() tend vers 0 lorsque
tend vers 0 lorsque ![]() tend vers
tend vers ![]() . Cette vidéo donne une preuve détaillée de ce résultat très classique.
. Cette vidéo donne une preuve détaillée de ce résultat très classique.
Si une fonction ![]() est dérivable sur un intervalle et si
est dérivable sur un intervalle et si ![]() est positive, alors
est positive, alors ![]() est croissante. Et si
est croissante. Et si ![]() est strictement positive, alors
est strictement positive, alors ![]() est strictement croissante. Cette vidéo commence par établir ces résultats fondamentaux puis creuse le sujet …
est strictement croissante. Cette vidéo commence par établir ces résultats fondamentaux puis creuse le sujet …
Que pourrait-on bien dire, du point de vue arithmétique, concernant l’entier 2023 ?
Pour le savoir, il faut cliquer 🙂
Quatre preuves de la non-dénombrabilité de ![]() , parmi lesquelles la célèbre preuve de Cantor qui fait intervenir le procédé diagonal. Ces démonstrations détaillées sont précédées d’une courte introduction à la notion de dénombrabilité.
, parmi lesquelles la célèbre preuve de Cantor qui fait intervenir le procédé diagonal. Ces démonstrations détaillées sont précédées d’une courte introduction à la notion de dénombrabilité.
Notion de série numérique absolument convergente et deux preuves du théorème de convergence absolue. Trois exemples d’utilisation, de difficulté graduée. Quelques mots sur les séries semi-convergentes et notamment la série harmonique alternée.
Cette vidéo propose la preuve détaillée d’un célèbre développement asymptotique : celui de l’expression 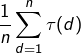 , où
, où ![]() désigne le nombre de diviseurs de
désigne le nombre de diviseurs de ![]() . Ce résultat, est dû à Dirichlet et fait intervenir la constante d’Euler.
. Ce résultat, est dû à Dirichlet et fait intervenir la constante d’Euler.
π et e sont sans doute les deux constantes mathématiques les plus célèbres. Ensuite, arrivent probablement le nombre d’or et … la constante d’Euler. C’est à cette dernière, notée par la minuscule grecque γ (gamma) qu’est consacrée cette vidéo.
On note classiquement ![]() le nombre de diviseurs de l’entier positif
le nombre de diviseurs de l’entier positif ![]() . Cette vidéo aborde modestement l’étude asymptotique de cette fonction arithmétique. On y montre notamment que
. Cette vidéo aborde modestement l’étude asymptotique de cette fonction arithmétique. On y montre notamment que ![]() , lorsque
, lorsque ![]() , pour tout
, pour tout ![]() .
.
Les sous-groupes additifs de ![]() se répartissent en deux classes : les sous-groupes discrets, de la forme
se répartissent en deux classes : les sous-groupes discrets, de la forme ![]() , avec
, avec ![]() et les sous-groupes denses (parmi lesquels on trouve
et les sous-groupes denses (parmi lesquels on trouve ![]() ,…). C’est de cette question que traite cette vidéo.
,…). C’est de cette question que traite cette vidéo.
Pour tout ensemble fini ![]() de nombres premiers, il existe un nombre premier qui n’appartient pas à
de nombres premiers, il existe un nombre premier qui n’appartient pas à ![]() . C’est ainsi qu’Euclide démontra, il y a 24 siècles, l’existence d’une infinité de nombres premiers. Cinq autres preuves de ce résultat sont rassemblées ici.
. C’est ainsi qu’Euclide démontra, il y a 24 siècles, l’existence d’une infinité de nombres premiers. Cinq autres preuves de ce résultat sont rassemblées ici.
Quelques propriétés généralement méconnues de la suite de Fibonacci … Par exemple : il existe une formule de récurrence du premier ordre pour cette suite ! Ou encore : les seuls carrés parfait figurant dans la suite sont 0, 1 et 144.
Une initiation, tout en douceur, à la théorie des enveloppes.
Au menu : une parabole, une cardioïde et une deltoïde !
L’entier 2022 est remarquable par l’un de ses facteurs premiers.
Pour en savoir davantage, il faut cliquer 🙂
La somme de la série ![]() a constitué, vers le milieu du XVII-ème siècle, un énigme apparemment insoluble pour les meilleurs esprits de l’époque. C’est à Leonhard EULER que l’on doit la solution de cette question passionnante.
a constitué, vers le milieu du XVII-ème siècle, un énigme apparemment insoluble pour les meilleurs esprits de l’époque. C’est à Leonhard EULER que l’on doit la solution de cette question passionnante.
Trois exercices corrigés autour des formules de transformations de sommes en produits et inversement. Comme celle-ci :
![]()
Combien la somme ![]() comporte-t-elle de termes ?
comporte-t-elle de termes ?
La réponse est donnée par le « théorème des petites voitures » 🙂
Est-ce que 0,999… (avec une infinité de chiffres ‘9’) est égal à 1 ?
Cette vidéo apporte une réponse en replaçant la question dans son contexte : la notion de développement décimal propre d’un nombre réel.
Trois exercices corrigés de trigonométrie.
Thème – Les formules d’addition :
![]()
Formules d’addition du sinus, du cosinus et de la tangente. Formules de duplication. Calcul de la limite en 0 de ![]() . Application à la dérivation de
. Application à la dérivation de ![]() ,
, ![]() et
et ![]() .
.
Premier épisode d’une vidéo en deux parties, consacrée aux bases de la trigonométrie circulaire. Définition du cosinus et du sinus, formule ![]() , cas d’égalité, formules de symétrie et valeurs remarquables, sans oublier la tangente.
, cas d’égalité, formules de symétrie et valeurs remarquables, sans oublier la tangente.
L’objet de cette vidéo est le calcul de ![]() , pour tout entier
, pour tout entier ![]() . Le résultat obtenu donne accès au calcul de
. Le résultat obtenu donne accès au calcul de ![]() . Une méthode plus directe pour le calcul de cette intégrale impropre est aussi proposé.
. Une méthode plus directe pour le calcul de cette intégrale impropre est aussi proposé.
Les nombres premiers fascinent les mathématiciens depuis toujours. Cette vidéo propose un premier contact avec cette notion, simple en apparence … mais en apparence seulement
Preuves rigoureuses de quatre formules fondamentales de combinatoire : le calcul des nombres de parties, d’applications, d’injections et d’applications strictement croissantes.
Un thème classique de combinatoire : le calcul du nombre ![]() de surjections de X vers Y, où X et Y sont deux ensembles finis, de cardinaux respectifs
de surjections de X vers Y, où X et Y sont deux ensembles finis, de cardinaux respectifs ![]() :
: 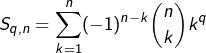
Espaces vectoriels de dimension finie.
Principales méthodes pour le calcul d’une dimension.
Les détails sont consultables dans cet article.
4 exercices sont corrigés en détail.
Espaces vectoriels de dimension finie.
Existence de bases via le théorème de la base incomplète.
Dimension d’un sous-espace vectoriel.
Espaces vectoriels de dimension finie.
Un exemple introductif suivi du début de la théorie, avec le lemme de Steinitz. On en déduit que toutes les bases comportent le même nombre de vecteurs.
Supplémentaire orthogonal d’un sous-espace de dimension finie. Projecteurs orthogonaux et leur caractérisation parmi les projecteurs. Distance d’un vecteur à un sev de dimension finie dans un espace préhilbertien réel.
Deux exemples explicites de projecteurs. Projecteurs et symétries. Mise en évidence d’une base de ![]() exclusivement composée de projecteurs.
exclusivement composée de projecteurs.
On définit ce qu’est le projecteur p sur F parallèlement à G, où F et G sont deux sev supplémentaires dans un ![]() -ev E. On met ensuite en évidence les principales propriétés de p.
-ev E. On met ensuite en évidence les principales propriétés de p.
Après avoir rappelé ce que sont les nombres rationnels et irrationnels, on prouve successivement l’irrationalité de e puis de π. En fin de vidéo on démontre, en admettant la transcendance de e et π, que l’un au moins des nombres e+π et eπ est irrationnel.
CONSEILS MÉTHODOLOGIQUES
Trois vidéos d’une dizaine de minutes chacune, principalement destinées aux étudiants de CPGE scientifiques et de licence de math / info.
On y aborde la question, souvent posée, des méthodes à mettre en œuvre pour étudier efficacement les mathématiques à ce niveau.
Comment et à quel rythme étudier le cours ?
Les exercices d’abord et le cours ensuite, ou l’inverse ?
Pourquoi est-il si important d’apprendre à rédiger ?
Comment faire pour mémoriser à long terme ? …
AUTRES VIDÉOS
Le logiciel Live Iteration ! permet l’étude interactive des suites définies par une relation de récurrence de la forme ![]() avec
avec ![]() donné et
donné et ![]() un paramètre. Cette vidéo en donne un mode d’emploi, illustré d’exemples.
un paramètre. Cette vidéo en donne un mode d’emploi, illustré d’exemples.
L’objet de cette vidéo est la résolution commentée d’un exercice de topologie. On s’intéresse à l’union d’une famille dénombrable de disques fermés. S’agit-il d’une partie fermée du plan ?
Etant donnés des réels ![]() tous distincts et des réels
tous distincts et des réels ![]() quelconques, il existe un unique d’un polynôme
quelconques, il existe un unique d’un polynôme ![]() de degré au plus
de degré au plus ![]() vérifiant
vérifiant ![]() pour tout
pour tout ![]() . C’est le polynôme interpolateur de Lagrange. On décrit ensuite, sans démonstration, le phénomène de Runge.
. C’est le polynôme interpolateur de Lagrange. On décrit ensuite, sans démonstration, le phénomène de Runge.
La convexité de la fonction exponentielle est évidente si l’on regarde sa dérivée seconde. Mais on peut peut aussi (exercice de style …) l’établir en revenant à la définition de la convexité et en utilisant astucieusement le lemme de Rolle.
La formule ![]() est valable pour tout couple
est valable pour tout couple ![]() de réels positifs. Elle est historiquement liée à l’élaboration, par des mathématiciens du 18ème siècle, de méthodes de calcul approché de
de réels positifs. Elle est historiquement liée à l’élaboration, par des mathématiciens du 18ème siècle, de méthodes de calcul approché de ![]() .
.
Une formule explicite pour ![]() .
.
Contrairement à ce qu’on pourrait penser, cette expression ne se réduit pas bêtement à ![]() …!
…!

La partie entière d’un réel x est le plus grand entier relatif inférieur ou égal à x. Elle est notée ![]() .
.
Par exemple : ![]()
Cette vidéo présente les principales propriétés de cette fonction.
Lorsqu’on immerge dans de l’eau savonneuse la structure très simple décrite dans cette vidéo puis qu’on la retire délicatement, on observe l’apparition d’un film de savon dont l’aire doit être minimale …
Exercice d’oral type X-ENS.
Si ![]() est continue et si
est continue et si ![]() est uniformément continue, alors
est uniformément continue, alors ![]() est aussi uniformément continue.
est aussi uniformément continue.
Tout entier ![]() s’écrit de manière unique :
s’écrit de manière unique : 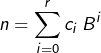
où ![]() est la base et les
est la base et les ![]() sont les chiffres.
sont les chiffres.
Exemples, remarques et programme de conversion en Python3.
L’itération des polynômes du type ![]() donne naissance à de prodigieux ensembles présentant une structure fractale !
donne naissance à de prodigieux ensembles présentant une structure fractale !
Pour tout entier ![]() , l’équation
, l’équation ![]() possède
possède ![]() solutions distinctes dans
solutions distinctes dans ![]() .
.
Ce sont les racines ![]() èmes de l’unité, données par :
èmes de l’unité, données par :
![]()
Le lemme de décomposition des noyaux est un outil essentiel pour l’étude de la réduction des endomorphismes.
Il permet de décomposer le noyau de ![]() en la somme directe de noyaux similaires, associés à des facteurs de
en la somme directe de noyaux similaires, associés à des facteurs de ![]() , deux à deux premiers entre eux.
, deux à deux premiers entre eux.
Tout ![]() peut s’écrire
peut s’écrire ![]() avec
avec ![]() et
et ![]() . Un tel
. Un tel ![]() est un argument de
est un argument de ![]() .
.
Comment calculer les arguments de ![]() à partir de ses parties réelle et imaginaire ? Et pour l’argument principal ?
à partir de ses parties réelle et imaginaire ? Et pour l’argument principal ?
Si ![]() est un groupe fini et si
est un groupe fini et si ![]() est un sous-groupe de
est un sous-groupe de ![]() , alors le cardinal de
, alors le cardinal de ![]() divise celui de
divise celui de ![]() .
.
Une conséquence : si ![]() est un groupe fini et si
est un groupe fini et si ![]() , alors l’ordre de
, alors l’ordre de ![]() est un diviseur de
est un diviseur de ![]() .
.
Trois exercices assez jolis, de niveau MPSI / PCSI / MPII / L1 Maths, autour de l’inégalité triangulaire.
Pour tout couple ![]() de nombre complexes :
de nombre complexes :
![]()
Dans cette vidéo, on prouve cette célèbre inégalité et précisant le cas d’égalité.
Définition de la notion de dérivabilité en un point, pour une fonction numérique. Taux d’accroissement, nombre dérivé, équation de la tangente, etc …
Un joli exercice de recherche du spectre d’un endomorphisme en dimension infinie.
L’ensemble des valeurs propres du « shift » est ![]() .
.
Intégrales de Wallis : Partie 3.
Convergence vers 0 revisitée, avec ![]() et
et ![]() …
…
ou par majoration explicite de ![]() .
.
Preuve « instantanée » via le théorème de convergence dominée.
La fonction logarithme, introduite comme étant la primitive de ![]() qui s’annule en 1.
qui s’annule en 1.
Principales propriétés : sens de variation, équation fonctionnelle, limites usuelles, etc …
Formule ![]() , Irrationalité de
, Irrationalité de ![]() .
.
Comparaison des moyennes arithmétique et géométrique de deux réels positifs.
Calcul approché d’une racine carrée par dichotomie
Approximation de ![]() pour
pour ![]() « petit ».
« petit ».
Existence de la racine carrée
Qu’est-ce qu’une identité remarquable et à quoi cela peut-il bien servir ?
A factoriser, développer, comparer, transformer … mais aussi à faire un peu de calcul mental 🙂
ANCIENNES VIDÉOS
Correspondances : Partie 1
Notion générale de correspondance.
Images et antécédents. Fonctions et applications.
Equations du second degré : Partie 1.
Exemples préliminaires.
Mise sous forme canonique et discussion selon le signe du discriminant. Le nombre d’or vite fait …
Equations du second degré : Partie 2.
Lecture graphique du nombre de solution.
Lieu du sommet de la parabole d’équation ![]() lorsque
lorsque ![]() varie (
varie (![]() et
et ![]() étant fixés,
étant fixés, ![]() ).
).
Equations du second degré : Partie 3.
Etude dans le champ complexe.
Méthode pratique pour le calcul, sous la forme ![]() avec
avec ![]() réels, des racines carrées d’un nombre complexe.
réels, des racines carrées d’un nombre complexe.


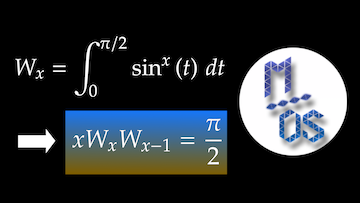

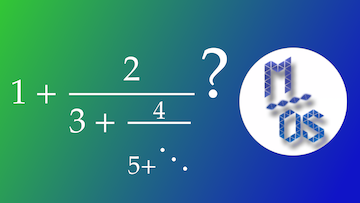



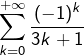 puis à la recherche d’un équivalent de
puis à la recherche d’un équivalent de 
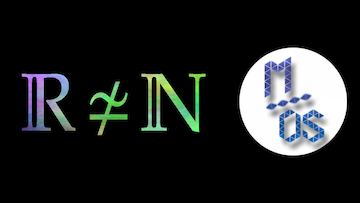

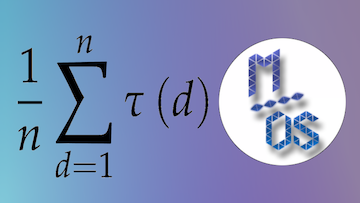

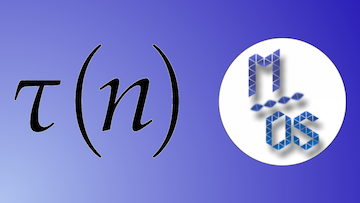
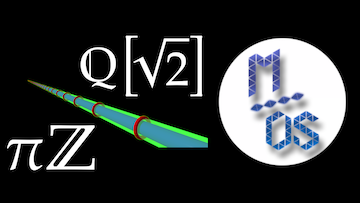


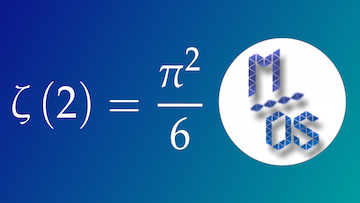































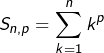 est un multiple de
est un multiple de 
![Rendered by QuickLaTeX.com \[S_{n,p}=\sum_{k=1}^nk^p\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bf2498debb88463b2ab0c6380650512e_l3.png)

![Rendered by QuickLaTeX.com \[\sum_{k=1}^nk\,\binom{n}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-da2f1f227d47fbbd81107bc852c28f31_l3.png)

















