Solutions - Exercices sur les séries numériques - 01

Pour tout couple $\left(x,y\right)$ de réels :

$\left|xy\right|\leqslant\frac{1}{2}\left(x^{2}+y^{2}\right)$

Cette inégalité n’est qu’une reformulation de la relation $\left(\left|x\right|-\left|y\right|\right)^{2}\geqslant0.$

En remplaçant $x$ et $y$ par $a_{n}$ et $1/n$ respectivement, on voit que, pour tout $n\in\mathbb{N}^{\star}$ :

$\left|\frac{a_{n}}{n}\right|\leqslant\frac{1}{2}\left(a_{n}^{2}+\frac{1}{n^{2}}\right)$

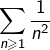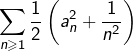Comme la série $\sum_{n\geqslant1}\frac{1}{n^2}$ est convergente et vu que la série $\sum_{n\geqslant1}a_{n}^{2}$ converge par hypothèse, on conclut dans un premier temps que la série $\sum_{n\geqslant1}\frac{1}{2}\left(a_{n}^{2}+\frac{1}{n^{2}}\right)$ converge, puis (avec le principe de comparaison) que la série $\sum_{n\geqslant1}\frac{a_{n}}{n}$ est absolument convergente (donc convergente).

Plus généralement (et par le même argument ) : si les séries $\sum_{n\geqslant1}a_{n}^{2}$ et $\sum_{n\geqslant1}b_{n}^{2}$ convergent, alors la série $\sum_{n\geqslant1}a_{n}b_{n}$ est absolument convergente.

Ceci permet de définir un produit scalaire sur l’espace vectoriel des suites réelles de carré sommable, traditionnellement noté $\ell_{2}\left(\mathbb{R}\right).$ Il suffit de poser, pour tout $\left(a,b\right)\in\ell_{2}\left(\mathbb{R}\right)^{2}$ :

$\left(a\mid b\right)=\sum_{n=1}^{\infty}a_{n}b_{n}$

On peut montrer, en outre, que $\ell_{2}\left(\mathbb{R}\right)$ est un espace de Hilbert (c’est-à-dire qu’il est complet pour la norme induite par ce produit scalaire).

En supposant que la série $\sum_{n\geqslant0}a_{n}$ converge, il suffit de voir que :

$\forall n\in\mathbb{N},\thinspace0\leqslant\frac{a_{n}}{1+a_{n}}\leqslant a_{n}$

pour conclure (avec le principe de comparaison) que la série $\sum_{n\geqslant0}\frac{a_{n}}{1+a_{n}}$ converge aussi.

On peut aussi invoquer la règle des équivalents puisque, vu que $\lim_{n\rightarrow\infty}a_{n}=0$ (condition nécessaire de convergence), on a :

$\frac{a_{n}}{1+a_{n}}\sim a_{n}\quad\text{lorsque }n\rightarrow\infty$

Réciproquement, supposons la convergence de la série ${\displaystyle \sum_{n\geqslant0}\frac{a_{n}}{1+a_{n}}}.$ En posant, pour tout $n\in\mathbb{N}$ :

$b_{n}=\frac{a_{n}}{1+a_{n}}$

il est clair que $b_{n}\neq1$ et qu’on peut donc écrire :

$a_{n}=\frac{b_{n}}{1-b_{n}}$

Comme $\lim_{n\rightarrow\infty}b_{n}=0$ (condition nécessaire de convergence, à nouveau), on voit que $a_{n}\sim b_{n}$ et la convergence de la série $\sum_{n\geqslant0}a_{n}$ en résulte.

C’est VRAI. En effet, pour tout $n\in\mathbb{N}$ :

$0\leqslant b_{n}-a_{n}\leqslant c_{n}-a_{n}$

or la série $\sum_{n\geqslant0}\left(c_{n}-a_{n}\right)$ converge (différence de deux séries convergentes) et donc, d’après le principe de comparaison, la série $\sum_{n\geqslant0}\left(b_{n}-a_{n}\right)$ converge aussi. Ainsi, la série $\sum_{n\geqslant0}a_{n}$ apparaît comme la différence de deux séries convergentes, à savoir $\sum_{n\geqslant0}b_{n}$ et ${\displaystyle \sum_{n\geqslant0}\left(b_{n}-a_{n}\right)}.$

Pour tout couple $\left(r,s\right)$ de réels strictement positifs :

$r^{\ln\left(s\right)}=e^{\ln\left(r\right)\ln\left(s\right)}=s^{\ln\left(r\right)}$

En appliquant ceci au couple $\left(r,s\right)=\left(\ln\left(n\right),n\right),$ il vient :

$\forall n\geqslant2,\:\frac{1}{\ln\left(n\right)^{\ln\left(n\right)}}=\frac{1}{n^{\ln\left(\ln\left(n\right)\right)}}$

Il est maintenant clair que :

$\boxed{\frac{1}{n^{\ln\left(\ln\left(n\right)\right)}}\leqslant\frac{1}{n^{2}}}$

dès que $n$ est assez grand (pour être précis, dès que $n\geqslant1619$ puisque $e^{e^{2}}\simeq1618,2$ à $10^{-1}$ près).

Finalement, d’après le principe de comparaison, la série proposée converge.

Posons, pour tout $n\in\mathbb{N}^{\star}$ :

$S_{n}=\sum_{k=1}^{n}\frac{1}{k\thinspace2^{k}}$

A l’aide de l’indication, on trouve une expression intégrale pour cette somme partielle :

$\begin{eqnarray*}S_{n} & = & \sum_{k=1}^{n}\int_{0}^{1/2}t^{k-1}\thinspace dt\\& = & \int_{0}^{1/2}\sum_{k=1}^{n}t^{k-1}\thinspace dt\\& = & \int_{0}^{1/2}\frac{1-t^{n}}{1-t}\thinspace dt\end{eqnarray*}$

et donc :

$S_{n}=\ln\left(2\right)-\int_{0}^{1/2}\frac{t^{n}}{1-t}\thinspace dt$

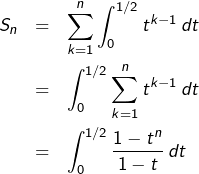
Il suffit alors de voir que :

$0\leqslant\int_{0}^{1/2}\frac{t^{n}}{1-t}\thinspace dt\leqslant2\int_{0}^{1/2}\thinspace t^{n}\thinspace dt=\frac{1}{\left(n+1\right)\thinspace2^{n}}$

pour conclure que :

$\lim_{n\rightarrow\infty}\int_{0}^{1/2}\frac{t^{n}}{1-t}\thinspace dt=0$

Ainsi, la série la série 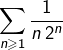$\sum_{n\geqslant1}\frac{1}{n\thinspace2^{n}}$ converge et admet pour somme :

$\boxed{\sum_{n=1}^{\infty}\frac{1}{n\thinspace2^{n}}=\ln\left(2\right)}$

Dans l’exercice précédent, on a obtenu une formule intégrale pour le reste :

$R_{n}=\sum_{k=n+1}^{\infty}\frac{1}{k\thinspace2^{k}}$

à savoir :

$R_{n}=\int_{0}^{1/2}\frac{t^{n}}{1-t}\thinspace dt$

ainsi que l’encadrement :

$0\leqslant R_{n}\leqslant\frac{1}{\left(n+1\right)\thinspace2^{n}}$

Autrement dit, pour tout $n\in\mathbb{N}^{\star}$ :

$0\leqslant\ln\left(2\right)-S_{n}\leqslant\frac{1}{\left(n+1\right)\thinspace2^{n}}$

On peut donc affirmer que $S_{n}$ sera une valeur approchée (par
défaut) de $\ln\left(2\right)$ à $10^{-7}$ près, dès que la condition

$\frac{1}{\left(n+1\right)\thinspace2^{n}}\leqslant10^{-7}$

est remplie, ce qui équivaut bien sûr à :

$\left(n+1\right)\thinspace2^{n}\geqslant10^{7}$

Avec Python, on peut écrire une fonction qui renvoie le plus petit entier naturel vérifiant ce type de condition :

def seuil(p):
    n = 0
    while ((n+1) * 2**n < 10**p):
        n += 1
    return n

On obtient ainsi :

>>> seuil(7)
    19

Ensuite, il nous faut une fonction qui calcule la somme partielle $S_{n}$ pour un entier $n\geqslant1$ donné. On peut utiliser le module fractions pour calculer les sommes partielles de manière exacte :

from fractions import Fraction

def sommePartielle(n):
    s = Fraction()
    for k in range (1,n+1):
        s += Fraction(1, k * 2**k)
    return s

Et voici le résultat :

>>> sommePartielle(19)
    Fraction(10574855234543, 15256293212160)

qu’on peut d’ailleurs vérifier (le symbole _ fait référence au résultat précédemment calculé par l’interpréteur Python) :

>>> log(2) - _
    9.119263222334695e-08

Tout ceci montre que le rationnel

$S_{19}=\frac{10\thinspace574\thinspace855\thinspace234\thinspace543}{15\thinspace256\thinspace293\thinspace212\thinspace160}$

est une valeur approchée par défaut à $10^{-7}$ près de $\ln\left(2\right)$ .

Et si l’on veut on écriture décimale approchée :

>>> float(sommePartielle(19))
    0.6931470893673131

d’où finalement :

$\boxed{0,6931470<\ln\left(2\right)<0,6931471}$

Supposons $\boxed{\alpha>1}$ et soit $\beta\in\left]1,\alpha\right[.$ Alors pour $N$ convenable et tout $n\geqslant N$ :

$\frac{\ln\left(\frac{1}{a_{n}}\right)}{\ln\left(n\right)}\geqslant\beta$

ou encore :

$a_{n}\leqslant\frac{1}{n^{\beta}}$

d’où la convergence de la série $\sum_{n\geqslant1}\,a_{n}.$

Si $\boxed{\alpha<1}$ , alors à partir d’un certain rang :

$\frac{\ln\left(\frac{1}{a_{n}}\right)}{\ln\left(n\right)}\leqslant1$

c’est-à-dire :

$a_{n}\geqslant\frac{1}{n}$

d’où la divergence de la série $\sum_{n\geqslant1}\,a_{n}.$

En revanche, on ne peut rien dire si $\boxed{\alpha=1}.$ En effet (dans ce qui suit, on suppose connues les séries de Bertrand) en choisissant :

$a_{n}=\frac{1}{n\ln\left(n\right)}$

on voit que :

$\frac{\ln\left(\frac{1}{a_{n}}\right)}{\ln\left(n\right)}=1+\frac{\ln\left(\ln\left(n\right)\right)}{\ln\left(n\right)}\rightarrow1$

et la série $\sum_{n\geqslant2}a_{n}$ diverge; tandis que pour :

$a_{n}=\frac{1}{n\ln^{2}\left(n\right)}$

on a encore :

$\frac{\ln\left(\frac{1}{a_{n}}\right)}{\ln\left(n\right)}=1+\frac{2\thinspace\ln\left(\ln\left(n\right)\right)}{\ln\left(n\right)}\rightarrow1$

mais cette fois, la série $\sum_{n\geqslant2}a_{n}$ converge.

Une version plus simple de cet exercice consiste à calculer explicitement :

$A=\sum_{n=0}^{\infty}\frac{1}{\left(2n\right)!}$

Si vous connaissez le développement en série entière de la fonction cosinus hyperbolique, alors tout est dit :

$A=\frac{1}{2}\left(e+\frac{1}{e}\right)$

Mais on peut totalement se passer de cela et c’est même mieux, si l’on veut comprendre ce qui se passe. L’idée est d’ajouter membre à membre les égalités :

$e=\exp\left(1\right)=\sum_{n=0}^{\infty}\frac{1}{n!}$

$\frac{1}{e}=\exp\left(-1\right)=\sum_{n=0}^{\infty}\frac{\left(-1\right)^{n}}{n!}$

Les termes d’indice impair se neutralisent et il reste le double de
la série des termes d’indice pair, d’où le résultat.

Le fait que $-1$ soit un nombre dont la suite des puissances est de période 2 joue ici un rôle crucial. Il est donc naturel de chercher un nombre dont la suite des puissances serait de période 3.

Eh bien justement, nous connaissons un tel nombre ! Il s’agit de :

$j=e^{2i\pi/3}$

qui est l’une des racines cubiques de l’unité. Ajoutons donc, membre à membre, les trois égalités suivantes :

$\left\{ \begin{array}{ccc} e & = & {\displaystyle \sum_{n=0}^{\infty}\frac{1}{n!}}\\\\e^{j} & = & {\displaystyle \sum_{n=0}^{\infty}\frac{j^{n}}{n!}}\\\\e^{j^{2}} & = & {\displaystyle \sum_{n=0}^{\infty}\frac{j^{2n}}{n!}} \end{array}\right.$

Au membre de droite, on obtient le nombre complexe :

$\sum_{n=0}^{\infty}\frac{1+j^{n}+j^{2n}}{n!}$

Si l’on pose, pour tout $n\in\mathbb{N}$ :

$z_{n}=1+j^{n}+j^{2n}$

alors, d’après de la formule bien connue $1+j+j^{2}=0$ :

$z_{n}=\left\{ \begin{array}{cc}3 & \text{si }n\equiv0\pmod{3}\\\\0 & \text{sinon}\end{array}\right.$

Ainsi :

$\boxed{\sum_{n=0}^{\infty}\frac{1}{\left(3n\right)!}=\frac{1}{3}\left(e+e^{j}+e^{j^{2}}\right)}$

On peut améliorer un peu la forme du résultat. En effet :

$j=-\frac{1}{2}+i\frac{\sqrt{3}}{2}$

donc :

$e^{j}=\frac{1}{\sqrt{e}}\left(\cos\left(\frac{\sqrt{3}}{2}\right)+i\sin\left(\frac{\sqrt{3}}{2}\right)\right)$

et de même, comme $j^{2}$ n’est autre que le conjugué de $j$ :

$e^{j^{2}}=\frac{1}{\sqrt{e}}\left(\cos\left(\frac{\sqrt{3}}{2}\right)-i\sin\left(\frac{\sqrt{3}}{2}\right)\right)$

En conclusion :

$\boxed{\sum_{n=0}^{\infty}\frac{1}{\left(3n\right)!}=\frac{1}{3}\left(e+\frac{2}{\sqrt{e}}\cos\left(\frac{\sqrt{3}}{2}\right)\right)}$

Il est clair que $0\leqslant\left(1-t^{n}\right)^{1/n}\leqslant1,$ pour tout $\left(n,t\right)\in\mathbb{N}^{\star}\times\left[0,1\right].$ On peut donc considérer l’application :

$f_{n}:\left[0,1\right]\rightarrow\left[0,1\right],\thinspace t\mapsto\left(1-t^{n}\right)^{1/n}$

Il s’agit d’une involution (c’est-à-dire que $f_{n}\circ f_{n}=id_{\left[0,1\right]})$ et son graphe présente donc une symétrie par rapport à la droite $\Delta$ d’équation $y=x.$

Par ailleurs, $f_{n}$ est dérivable sur $\left[0,1\right[$ et pour tout $t$ dans cet intervalle :

$f_{n}'\left(t\right)=-t^{n-1}\,\left(1-t^{n}\right)^{\frac{1}{n}-1}\leqslant0$

ce qui montre que $f_{n}$ est décroissante.

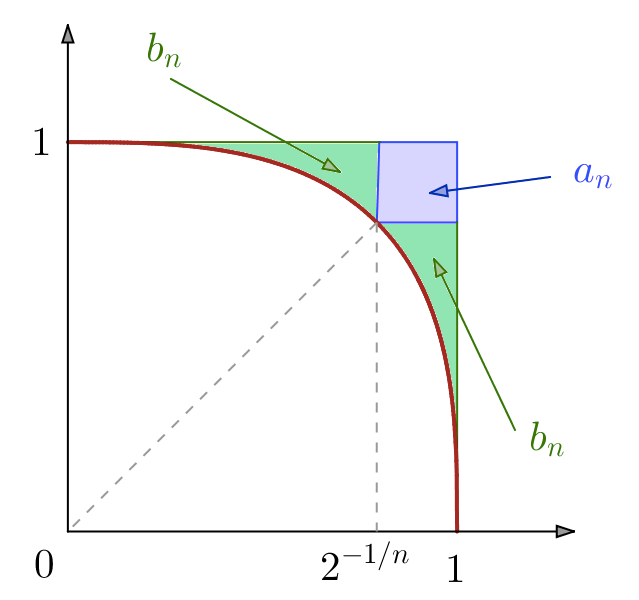
L’abscisse du point d’intersection entre le graphe de $f_{n}$ et $\Delta$ est :

$t_{n}=2^{-\frac{1}{n}}$

Notons $u_{n}$ le terme général de la série proposée :

$u_{n}=\int_{0}^{1}\left(1-\left(1-t^{n}\right)^{1/n}\right)\thinspace dt$

et notons encore :

$a_{n}$ est l’aire du carré bleu
$b_{n}$ est l’aire de chacune des régions vertes

de sorte que, pour tout $n\in\mathbb{N}^\star$ :

$\boxed{u_n=a_n+2\,b_n}$

➤ Montrons maintenant la convergence de chacune des séries

$\sum_{n\geqslant1}a_n\qquad\text{et}\qquad\sum_{n\geqslant1}b_n$

D’une part :

$\boxed{a_{n}=\left(1-t_{n}\right)^{2}\sim{\displaystyle \frac{\ln^{2}\left(2\right)}{n^{2}}}}$

ce qui prouve que la série $\sum_{n\geqslant1}a_{n}$ converge.

D’autre part :

$\begin{eqnarray*}b_{n} & = & \int_{0}^{t_{n}}\,\left(1-\left(1-t^{n}\right)^{\frac{1}{n}}\right)\,dt\\& = & \int_{0}^{t_{n}}\,\frac{t^{n}}{{\displaystyle \sum_{k=0}^{n-1}\,\left(1-t^{n}\right)^{\frac{k}{n}}}}\,dt\\& \leqslant & \frac{1}{{\displaystyle \sum_{k=0}^{n-1}\,2^{-\frac{k}{n}}}}\,\int_{0}^{t_{n}}\,t^{n}\,dt\end{eqnarray*}$

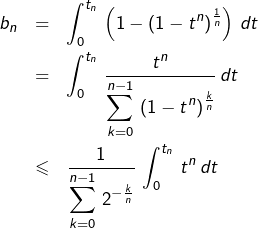
Mais :

$\sum_{k=0}^{n-1}\,2^{-\frac{k}{n}}}=\frac{1}{2}\left(1-2^{-\frac{1}{n}}\right)^{-1$

et :

$\int_{0}^{t_{n}}\,t^{n}\,dt=\frac{2^{-\frac{1}{n}}}{2\left(n+1\right)}$

donc :

$\boxed{b_{n}\leqslant\frac{2^{-1/n}\left(1-2^{-1/n}\right)}{n+1}\sim\frac{\ln\left(2\right)}{n^{2}}}$

ce qui prouve que la série $\sum_{n\geqslant1}\,b_{n}$ converge aussi.

Finalement, la série $\sum_{n\geqslant1}u_{n}$ converge.

Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.

Partager cet article

Laisser un commentaire Annuler la réponse