Solutions détaillées de neuf exercices sur raisonnement par récurrence (fiche 01).
Cliquer ici pour accéder aux énoncés.


Posons pour simplifier : ![]() pour tout
pour tout ![]()
D’une part : ![]() est multiple de
est multiple de ![]()
D’autre part, si pour un certain ![]() il existe
il existe ![]() tel que
tel que ![]() alors :
alors :
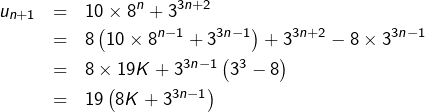
La propriété « ![]() est multiple de
est multiple de ![]() » est donc héréditaire. Comme elle est vraie pour
» est donc héréditaire. Comme elle est vraie pour ![]() alors elle est vraie pour tout
alors elle est vraie pour tout ![]()

Fixons ![]()
Au rang ![]() l’inégalité est claire :
l’inégalité est claire :
![]()
Supposons-la vraie au rang ![]() pour un certain entier
pour un certain entier ![]() En multipliant chaque membre de l’inégalité
En multipliant chaque membre de l’inégalité ![]() par le réel strictement positif
par le réel strictement positif ![]() on obtient :
on obtient :
![]()
c’est-à-dire :
![]()
et donc, a fortiori :
![]()

On effectue une récurrence d’ordre ![]() On l’initialise en calculant successivement :
On l’initialise en calculant successivement :
![]()
car
![]()
et
![]()
car
![]()
Passons à l’hérédité. Si, pour un certain ![]() on a
on a ![]() et
et ![]() alors :
alors :
![]()

On peut établir directement l’inégalité demandée en étudiant les variations de la fonction :
![]()
Il s’avère que celle-ci est croissante et donc majorée par sa limite en
![]()
(inégalité d’ailleurs valable pour tout
![Rendered by QuickLaTeX.com \[\boxed{\forall t>0,\left(1+\frac{1}{t}\right)^{t}<e}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6e52c999c66757e2fb11600f1aa8feb0_l3.png)
Prouvons maintenant que :
![]()
par récurrence.
Pour ![]() cette inégalité est vraie. Supposons-la vraie au rang
cette inégalité est vraie. Supposons-la vraie au rang ![]() alors :
alors :
![]()
![]()
![]()

Montrons par récurrence que pour tout entier ![]() et pour tout
et pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\prod_{k=1}^{n}\left(1-a_{k}\right)>1-\sum_{k=1}^{n}a_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-07324c981536296183624c0cd6712525_l3.png)
Pour ![]() c’est vrai; en effet :
c’est vrai; en effet :
![]()
Supposons le résultat établi au rang
![Rendered by QuickLaTeX.com \begin{eqnarray*}\left[\prod_{k=1}^{n}\left(1-a_{k}\right)\right]\left(1-a_{n+1}\right) & > & \left(1-\sum_{k=1}^{n}a_{k}\right)\left(1-a_{n+1}\right)\\& = & 1-\sum_{k=1}^{n+1}a_{k}+a_{n+1}\left(\sum_{k=1}^{n}a_{k}\right)\\& > & 1-\sum_{k=1}^{n+1}a_{k}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-090ff85d75ad8a4bf65f3d6a6b5c1649_l3.png)

On sait que si deux fonctions polynômes coïncident sur une partie infinie de ![]() alors elles sont égales (autrement dit : elles coïncident en tout point). Il en résulte que, pour un
alors elles sont égales (autrement dit : elles coïncident en tout point). Il en résulte que, pour un ![]() donné, un tel polynôme est unique : en effet, si
donné, un tel polynôme est unique : en effet, si ![]() et
et ![]() conviennent pour un même
conviennent pour un même ![]() alors :
alors :
![]()
et donc :
![]()
Pour l’existence, on procède par récurrence. Il est clair que :
![]()
et
![]()
Supposons (hypothèse de récurrence) que, pour un certain
![Rendered by QuickLaTeX.com \[\forall x\in\mathbb{R},\thinspace\left\{ \begin{array}{ccc}\sin\left(\left(n-1\right)x\right) & = & \sin\left(x\right)Q_{n-1}\left(\cos\left(x\right)\right)\\\\\sin\left(nx\right) & = & \sin\left(x\right)Q_{n}\left(\cos\left(x\right)\right)\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8d7ec0950235e1fbe61e711dcf32e84d_l3.png)
alors, d’après la …
Formule (transformation de somme en produit)
![]()
on voit que :
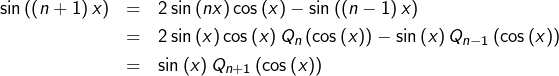
où l’on a posé :
On observe pour cela que, pour tout ![]() et pour tout
et pour tout ![]() :
:
![]()
or, d’après la formule de Moivre :
![]()
puis celle du binôme :
![Rendered by QuickLaTeX.com \[\left(\cos\left(x\right)+i\sin\left(x\right)\right)^{n+1}=\sum_{k=0}^{n+1}\binom{n+1}{k}\cos^{n+1-k}\left(x\right)\left(i\sin\left(x\right)\right)^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ee72894aaf9719aefe5ab6ce260b95cd_l3.png)
Dans cette dernière somme, les termes d’indices pairs sont réels et ceux d’indices impairs sont imaginaires purs; ainsi :
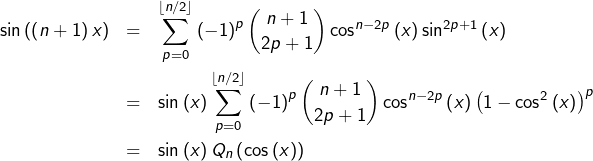
avec :
![Rendered by QuickLaTeX.com \[Q_{n}=\sum_{p=0}^{\left\lfloor n/2\right\rfloor }\left(-1\right)^{p}\binom{n+1}{2p+1}X^{n-2p}\left(1-X^{2}\right)^{p}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fd50d403640064a6ab00a5c688194ef6_l3.png)
ou encore :
![Rendered by QuickLaTeX.com \[\boxed{Q_{n}=\sum_{p=0}^{\left\lfloor n/2\right\rfloor }\binom{n+1}{2p+1}X^{n-2p}\left(X^{2}-1\right)^{p}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5d1048810312dd5e5963eba3ba85334d_l3.png)
Noter que cette preuve apporte aussi, mais sans récurrence, l’existence de

Question 1
Calcul de ![]() pour
pour ![]() :
:
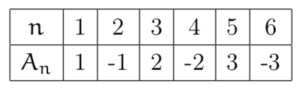
Question 2
L’égalité ![]() est vraie pour
est vraie pour ![]() :
:
![]()
Supposons-la vraie pour un certain ![]() alors :
alors :
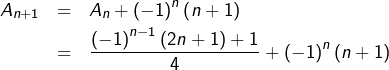
c’est-à-dire :
![]()
ou encore, comme souhaité :
![]()
On a établi par récurrence que :
![Rendered by QuickLaTeX.com \[ \boxed{\forall n\in\mathbb{N}^{\star},\thinspace\sum_{k=1}^{n}\left(-1\right)^{k-1}k=\frac{\left(-1\right)^{n-1}\left(2n+1\right)+1}{4}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-221fb0d1479b28fe5cad23f11a887247_l3.png)
Question 3
Soit ![]() Distinguons deux cas selon la parité de
Distinguons deux cas selon la parité de ![]() Si
Si ![]() est pair, alors en posant
est pair, alors en posant ![]() :
:
![]()
et
![]()
Et si
![]()
et
![]()
On a ainsi montré que :
![Rendered by QuickLaTeX.com \[ \boxed{\forall n\in\mathbb{N}^{\star},\thinspace\sum_{k=1}^{n}\left(-1\right)^{k-1}k=\left(-1\right)^{n-1}\left\lfloor \frac{n+1}{2}\right\rfloor }\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6f88f78838ab6838831dfe95f3ebf80c_l3.png)

On procède par récurrence. Pour ![]() la formule proposée donne :
la formule proposée donne :
![]()
et elle est donc vérifiée.
Supposons-la établie au rang ![]() alors pour tout
alors pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[g^{\left(n+1\right)}\left(x\right)=\left(-1\right)^{n}\left(n-1\right)!\,\sum_{k=1}^{n}\,\frac{\binom{n}{k}}{\left(k-1\right)!}\left[-\frac{n+k}{x^{n+k+1}}f^{\left(k\right)}\left(\frac{1}{x}\right)-\frac{1}{x^{n+k+2}}f^{\left(k+1\right)}\left(\frac{1}{x}\right)\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-94523626ecf4e062e6d96573c3488d59_l3.png)
On sépare la somme en deux, puis on ré-indexe la seconde en posant
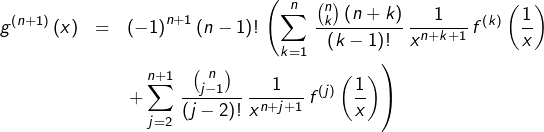
On isole alors, dans la première somme, le terme d’indice
![Rendered by QuickLaTeX.com \begin{eqnarray*}g^{\left(n+1\right)}\left(x\right) & = & \left(-1\right)^{n+1}\left(n-1\right)!\,\left(\frac{n\left(n+1\right)}{x^{n+2}}f'\left(\frac{1}{x}\right)+\frac{1}{\left(n-1\right)!\,x^{2n+2}}f^{\left(n+1\right)}\left(\frac{1}{x}\right)+\right.\\& & \left.\sum_{k=2}^{n}\,\frac{1}{\left(k-1\right)!}\left[\left(n+k\right)\binom{n}{k}+\left(k-1\right)\binom{n}{k-1}\right]\,\frac{1}{x^{n+k+1}}\,f^{\left(k\right)}\left(\frac{1}{x}\right)\right)\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-c22bcd163477398367e7a4f866be9800_l3.png)
Or :
![Rendered by QuickLaTeX.com \begin{eqnarray*}\left(n+k\right)\binom{n}{k}+\left(k-1\right)\binom{n}{k-1} & = & n!\,\left(\frac{n+k}{k!\,\left(n-k\right)!}+\frac{k-1}{\left(k-1\right)!\,\left(n-k+1\right)!}\right)\\& = & \frac{n!\left[\left(n+k\right)\left(n-k+1\right)+k\left(k-1\right)\right]}{k!\,\left(n-k+1\right)!}\\& = & n\,\binom{n+1}{k}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-9cbb5276ec69ccb013c84c989763fe6e_l3.png)
donc :
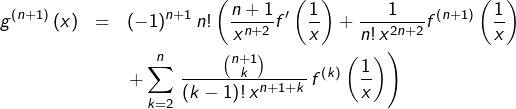
soit finalement :
![Rendered by QuickLaTeX.com \[g^{\left(n+1\right)}\left(x\right)=\left(-1\right)^{n+1}n!\,\sum_{k=1}^{n+1}\,\frac{\binom{n+1}{k}}{\left(k-1\right)!\,x^{n+1+k}}\,f^{\left(k\right)}\left(\frac{1}{x}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-757c3138c4341d4925f0e9969adc85e5_l3.png)
ce qui établit la formule au rang

On va établir la proposition suivante :
Soit ![]() et soient
et soient ![]() ses diviseurs. Notons
ses diviseurs. Notons ![]() le nombre de diviseurs de
le nombre de diviseurs de ![]() Alors :
Alors :
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{q}m_{i}^{3}=\left(\sum_{i=1}^{q}m_{i}\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6de442fbb35a4942c09c6bbcbfe28747_l3.png)
On raisonne par récurrence sur le nombre ![]() de facteurs premiers de
de facteurs premiers de ![]()
Pour ![]() il existe
il existe ![]() et
et ![]() tels que
tels que ![]() La liste des diviseurs de
La liste des diviseurs de ![]() est alors :
est alors :
![]()
et celle des nombres de diviseurs de chacun d’eux est :
![]()
Or il est classique que
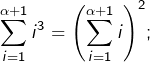 la propriété voulue est donc établie au rang
la propriété voulue est donc établie au rang Supposons la établie au rang ![]() pour un certain
pour un certain ![]()
Soit alors un entier naturel ![]() possédant
possédant ![]() facteurs premiers. On peut écrire
facteurs premiers. On peut écrire ![]() avec
avec ![]() possédant
possédant ![]() facteurs premiers,
facteurs premiers, ![]()
![]() et
et ![]()
Notons ![]() les diviseurs de
les diviseurs de ![]() et
et ![]() le nombre de diviseurs de
le nombre de diviseurs de ![]() pour tout
pour tout ![]()
Les diviseurs de ![]() sont alors les
sont alors les ![]() pour
pour ![]() et le nombre de diviseurs de
et le nombre de diviseurs de ![]() est
est ![]()
On constate alors que :
![Rendered by QuickLaTeX.com \begin{eqnarray*}\sum_{i=1}^{q}\left(\sum_{j=0}^{\alpha}\left(m_{i}\left(j+1\right)\right)^{3}\right) & = & \left(\sum_{i=1}^{q}m_{i}^{3}\right)\left(\sum_{j=1}^{\alpha+1}j^{3}\right)\\& \underset{{\scriptstyle {HR}}}{=} & \left(\sum_{i=1}^{q}m_{i}\right)^{2}\left(\sum_{j=1}^{\alpha+1}j\right)^{2}\\& = & \left[\sum_{i=1}^{q}\left(\sum_{j=0}^{\alpha}m_{i}\left(j+1\right)\right)\right]^{2}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-b6266dab2f728c4d375558fb6ae4d926_l3.png)
Ce résultat est attribué au mathématicien français Joseph Liouville (1809 – 1882).
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
