

Pour tout ![]() , d’après la formule du binôme :
, d’après la formule du binôme :
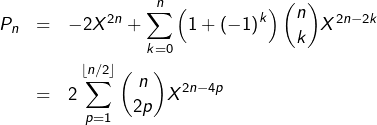
![]()

Pour tout ![]() l’évaluation en
l’évaluation en ![]() du polynôme
du polynôme
![Rendered by QuickLaTeX.com \[A_{n}=\sum_{k=0}^{n}\frac{\left(-1\right)^{k}}{k!}\prod_{j=0}^{k-1}\left(X-j\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f80354506f59880a35b9cb10f3e096e3_l3.png)
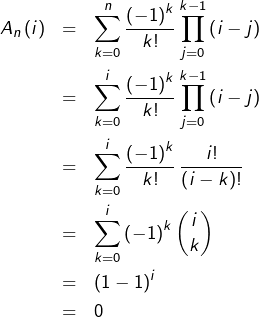
![Rendered by QuickLaTeX.com \[\boxed{A_{n}=\frac{\left(-1\right)^{n}}{n!}\prod_{k=1}^{n}\left(X-k\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1daab800c3d04a4bad80c9485b8a1828_l3.png)
Remarque
On peut aussi factoriser ![]()
![]() et
et ![]() puis formuler une conjecture et la valider en raisonnant par récurrence.
puis formuler une conjecture et la valider en raisonnant par récurrence.

Donnons deux preuves de ce résultat. La première sera constructive, contrairement à la seconde.
Preuve 1
Raisonnons par condition nécessaire. Si ![]() alors
alors ![]() convient (et c’est la seule possibilité). Sinon, notons
convient (et c’est la seule possibilité). Sinon, notons ![]() et observons que si
et observons que si ![]() convient alors
convient alors ![]() et :
et :

d’où, par sommation et vu que
![Rendered by QuickLaTeX.com \[P=\sum_{k=0}^{n}Q^{\left(k\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-16390313f5549b0b9a2a5a7557a28a49_l3.png)
Preuve 2
Après avoir traité le cas particulier où ![]() (cf. preuve n° 1), considérons l’endomorphisme
(cf. preuve n° 1), considérons l’endomorphisme ![]() et notons
et notons ![]()
Le sous-espace ![]() est stable par
est stable par ![]() et l’on dispose donc de l’endomorphisme induit
et l’on dispose donc de l’endomorphisme induit ![]()
Comme ![]() le théorème du rang assure que
le théorème du rang assure que ![]() est une bijection, d’où la conclusion.
est une bijection, d’où la conclusion.

Pour ![]() il suffit de voir que :
il suffit de voir que :
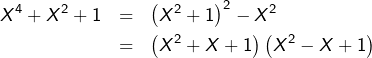
![]()
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{ccc}a+c & = & 0\\b+ac+d & = & 0\\ad+bc & = & 0\\bd & = & 1\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-92bddc1d465c00a605739eca41bec93c_l3.png)
![]()
![]()
Autre point de vue (plus « savant » et plus rapide). On observe que :
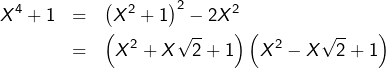

D’après la formule de Moivre :
![]()
![Rendered by QuickLaTeX.com \[\left(\cos\left(x\right)+i\sin\left(x\right)\right)^{n}=\sum_{k=0}^{n}\binom{n}{k}\cos^{n-k}\left(x\right)\left(i\sin\left(x\right)\right)^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5e88f0962f6351f58024a5307c50521b_l3.png)
![Rendered by QuickLaTeX.com \[\sin\left(nx\right)=\sum_{j=0}^{\left\lfloor \left(n-1\right)/2\right\rfloor }\left(-1\right)^{j}\binom{n}{2j+1}\cos^{n-2j-1}\left(x\right)\sin^{2j+1}\left(x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-266610374b57c01024cb041811036950_l3.png)
![Rendered by QuickLaTeX.com \[\sin\left(\left(2q+1\right)x\right)=\sum_{j=0}^{q}\left(-1\right)^{j}\binom{2q+1}{2j+1}\cos^{2q-2j}\left(x\right)\sin^{2j+1}\left(x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-45b638990ebdc2bb081564b564f71998_l3.png)
![]()
![Rendered by QuickLaTeX.com \[P_{2q+1}=\sum_{j=0}^{q}\left(-1\right)^{j}\binom{2q+1}{2j+1}\left(1-X^{2}\right)^{q-j}X^{2j+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c7a11aa305b6bf46c309c8e3053f2db8_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{P_{2q+1}=\left(-1\right)^{q}\sum_{j=0}^{q}\binom{2q+1}{2j+1}\left(X^{2}-1\right)^{q-j}X^{2j+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-24404a2e5ee2ae06067531b43ae60256_l3.png)
![]()
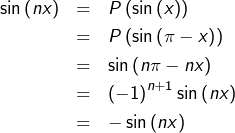

Parmi les polynômes constants, seul le polynôme nul convient (car ![]() est la seule solution de l’équation
est la seule solution de l’équation ![]() avec
avec ![]() Parmi les polynômes de degré 1, les seules solutions sont
Parmi les polynômes de degré 1, les seules solutions sont ![]() et
et ![]() En effet, si
En effet, si ![]() vérifie
vérifie
![]()
Et si
Supposons maintenant l’existence d’un polynôme solution ![]() de degré supérieur ou égal à
de degré supérieur ou égal à ![]() En dérivant chaque membre de l’équation fonctionnelle, on trouve, pour tout
En dérivant chaque membre de l’équation fonctionnelle, on trouve, pour tout ![]() :
:
(![]() )
) ![]()
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{c}\forall k\geqslant k_{0},\thinspace\left|P\left(x_{k}\right)\right|=2k\pi\\\\{\displaystyle \lim_{k\rightarrow\infty}\left|P'\left(x_{k}\right)\right|}=+\infty\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-eddb267ac9d2f4c676780cc04f513642_l3.png)
Si l’on pose :
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Soit ![]() tel que
tel que ![]() pour tout
pour tout ![]() Posons :
Posons :
![Rendered by QuickLaTeX.com \[P=\sum_{k=0}^{d}a_{k}X^{k}\qquad\text{avec }\forall k\in\left\llbracket 0,d\right\rrbracket ,\thinspace a_{k}\in\mathbb{Z}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6b101aadfdf5991d1a463efda53208b5_l3.png)
En choisissant ![]() dans ce qui précède, on voit que si
dans ce qui précède, on voit que si ![]() alors
alors ![]()
Mais comme ![]() et
et ![]() sont premiers, ils sont égaux ! Ainsi, le polynôme
sont premiers, ils sont égaux ! Ainsi, le polynôme ![]() est constant puisqu’il prend une infinité de fois la même valeur.
est constant puisqu’il prend une infinité de fois la même valeur.
Réciproquement, il est clair que les polynômes constants ![]() avec
avec ![]() conviennent !
conviennent !

Le polynôme nul convient. Si ![]() convient, alors en notant
convient, alors en notant ![]() et en choisissant
et en choisissant ![]() tous distincts (ce qui est possible vu que
tous distincts (ce qui est possible vu que ![]() est infini par hypothèse), on sait que :
est infini par hypothèse), on sait que :
![Rendered by QuickLaTeX.com \[P=\sum_{i=0}^{n}P\left(a_{i}\right)L_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b90f10dc9118a94fff73b307c532e382_l3.png)
![Rendered by QuickLaTeX.com \[L_{i}=\prod_{{0\leqslant j\leqslant n\atop j\neq i}}\frac{X-a_{j}}{a_{i}-a_{j}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4345276e7aab7d9a042077c28a4b2caa_l3.png)
![]()
![]()
En conclusion : les polynômes ![]() vérifiant
vérifiant ![]() pour une certaine partie infinie
pour une certaine partie infinie ![]() de
de ![]() sont exactement ceux à coefficients dans
sont exactement ceux à coefficients dans ![]()
Remarque
En particulier, les seuls ![]() vérifiant
vérifiant ![]() sont les éléments de
sont les éléments de ![]() De la même manière, les seuls
De la même manière, les seuls ![]() vérifiant
vérifiant ![]() sont les éléments de
sont les éléments de ![]()
Autre point de vue pour cette dernière affirmation : ![]() et
et ![]() (le polynôme conjugué de
(le polynôme conjugué de ![]() c’est-à-dire celui dont les coefficients sont les conjugués de ceux de
c’est-à-dire celui dont les coefficients sont les conjugués de ceux de ![]() coïncident sur
coïncident sur ![]() et comme
et comme ![]() est infini, alors
est infini, alors ![]() ce qui signifie exactement que
ce qui signifie exactement que ![]()
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
