

Le calcul des premiers termes de cette suite donne, successivement :
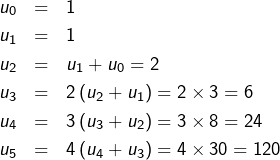
ce qui nous amène naturellement à conjecturer que :
![]()
Vue la manière dont cette suite ![]() a été définie, il s’agira d’une récurrence d’ordre 2.
a été définie, il s’agira d’une récurrence d’ordre 2.
Et comme l’initialisation est faite (largement), on peut passer à l’hérédité.
Supposons donc qu’on ait ![]() et
et ![]() pour un certain
pour un certain ![]()
Alors :
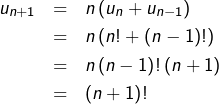

On calcule facilement :
![]()
![]()
![]()
![]()
On calcule ensuite :
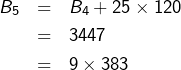
Une récurrence vient d’être initialisée. Supposons que, pour un certain ![]() on ait :
on ait : ![]()
Comme ![]() est multiple de
est multiple de ![]() alors
alors ![]() et donc
et donc ![]() puisque
puisque
![]()
![]()
On va utiliser la :
Proposition
Soit ![]() une suite de réels strictement positifs.
une suite de réels strictement positifs.
Si ![]() , alors :
, alors :
![]()
Ce résultat est une conséquence immédiate du lemme de Cesàro, appliqué à la suite ![]()
Cela dit, posons pour tout ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[\frac{x_{n+1}}{x_{n}}=\frac{\left(n+1\right)!}{\left(n+1\right)^{n+1}}\:\frac{n^{n}}{n!}=\left(\frac{n}{n+1}\right)^{n}=\left(1+\frac{1}{n}\right)^{-n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9c95278616037dc3e4557c18e343f299_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}\frac{\left(n!\right)^{1/n}}{n}=\frac{1}{e}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-69fb4937d0df9daf58887a7be92aca07_l3.png)

On observe que :
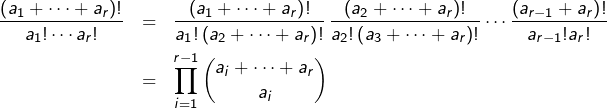
Remarque
Posons ![]() . Le nombre entier :
. Le nombre entier :
![]()
![]()
Etant donnés ![]() objets et
objets et ![]() cases numérotées de 1 à
cases numérotées de 1 à ![]() cet entier indique le nombre de façons de placer :
cet entier indique le nombre de façons de placer :
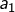 objets dans la case 1,
objets dans la case 1,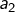 objets dans la case 2,
objets dans la case 2,- etc …,
- les
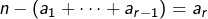 objets restants dans la case
objets restants dans la case 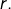
Lorsque ![]() (et donc
(et donc ![]() on retrouve le coefficient binomial ordinaire :
on retrouve le coefficient binomial ordinaire :
![]()

Si l’un des deux entiers ![]() ou
ou ![]() vaut 0 ou 1, le résultat est évidemment vrai.
vaut 0 ou 1, le résultat est évidemment vrai.
Supposons maintenant que ![]()
Alors ![]() car
car ![]() Il s’ensuit que
Il s’ensuit que ![]()
Par ailleurs ![]() puisque :
puisque :
![]()
![]()

Selon la formule du pion :
![]()
![]()
(![]() )
) ![Rendered by QuickLaTeX.com \[\boxed{n\mid\binom{nk}{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7dd910e52d6749f91108022912484bb8_l3.png)
![]()
![]()
![]()
![]()
![]()
L’inégalité ![]() est vraie pour
est vraie pour ![]() (c’est une égalité).
(c’est une égalité).
Supposons-la vraie pour un certain ![]() Alors :
Alors :
![]()
![]()
(![]() )
) ![]()
Or, la suite de terme général
![]()
![]()
On a prouvé par récurrence que :
![]()
Voici maintenant une autre preuve, plus élégante.
On observe que :
![Rendered by QuickLaTeX.com \[\left(2n\right)!=2n^{2}\prod_{k=1}^{n-1}k\left(2n-k\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-17d657cc3eefe865caf3e557da415239_l3.png)
![]()
![]()
Il en résulte que :
![]()

Commençons par établir le corollaire suivant de la formule de Legendre :
Corollaire
Etant donnés ![]() et
et ![]() on note
on note ![]() la somme des chiffres en base
la somme des chiffres en base ![]() de
de ![]() Alors :
Alors :
![]()
Preuve (cliquer pour déplier / replier)
Décomposons ![]() en base
en base ![]() :
:
![Rendered by QuickLaTeX.com \[n=\sum_{k=0}^{d}\,a_{k}p^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3ed1664ff588d247b862621a0cc5cf9b_l3.png)
![]()
(![]() )
) ![Rendered by QuickLaTeX.com \[\left\lfloor \frac{n}{p^{i}}\right\rfloor =\left\lfloor \sum_{k=i}^{d}\,a_{k}p^{k-i}+\sum_{k=0}^{i-1}\,a_{k}p^{k-i}\right\rfloor =\sum_{k=i}^{d}\,a_{k}p^{k-i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ebcec3c0c301f0bb91ddd8bf61249a93_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=i}^{d}\,a_{k}p^{k-i}\in\mathbb{N}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4f021054929ee4d2b0b1d321eca8e3b7_l3.png)
![Rendered by QuickLaTeX.com \[0\leqslant\sum_{k=0}^{i-1}\,a_{k}p^{k-i}\leqslant\left(p-1\right)\sum_{k=0}^{i-1}p^{k-i}<\left(p-1\right)\sum_{j=1}^{\infty}\frac{1}{p^{j}}=1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0c80fdcd8e4c1b5106ef500299843861_l3.png)
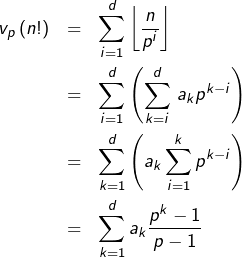
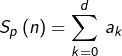 et la relation annoncée en résulte.
et la relation annoncée en résulte.
Venons-en maintenant à l’exercice. La condition ![]() équivaut à
équivaut à ![]()
Or, en remplaçant ![]() par 2 dans le corollaire ci-dessus :
par 2 dans le corollaire ci-dessus :
![]()
Ainsi, pour tout ![]() :
:
![]()
![]()

La formule de Legendre donne :
![Rendered by QuickLaTeX.com \[v_{p}\left(\frac{\left(30n\right)!\thinspace n!}{\left(15n\right)!\thinspace\left(10n\right)!\thinspace\left(6n\right)!}\right)=\sum_{k=1}^{\infty}\left(\left\lfloor \frac{30n}{p^{k}}\right\rfloor +\left\lfloor \frac{n}{p^{k}}\right\rfloor -\left\lfloor \frac{15n}{p^{k}}\right\rfloor -\left\lfloor \frac{10n}{p^{k}}\right\rfloor -\left\lfloor \frac{6n}{p^{k}}\right\rfloor \right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7ac4492059b51375dd55e2e13542271b_l3.png)
![]()
Soit donc ![]() et soit
et soit ![]() Alors :
Alors :
![]()
On constate, à chaque fois, la positivité de ![]() :
:
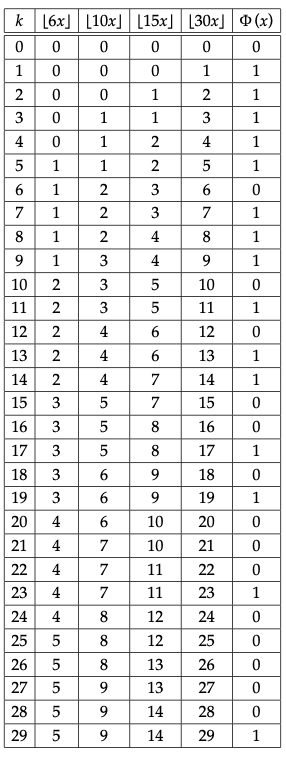
On notera que la fonction ![]() est à valeurs dans
est à valeurs dans ![]() .
.
Cette fonction a été utilisée par le mathématicien russe P. Tchebytchev pour établir le théorème selon lequel, pour tout ![]() :
:
![]()
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
