
Pour tout ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^{n}k\thinspace k!=\left(n+1\right)!-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1270d90d740efc7d11dd0892673cb7ae_l3.png)
En multipliant numérateur et dénominateur par le produit des nombres pairs de ![]() à
à ![]() on fait apparaître une factorielle au numérateur :
on fait apparaître une factorielle au numérateur :
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{Q_{n}=\frac{\left(2n\right)!}{4^{n}\thinspace\left(n!\right)^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-277504fe4cd84e80224b887237c98f65_l3.png)
Les deux fonctions suivantes calculent respectivement, étant donné un entier positif ou nul ![]() la factorielle et le nombre de chiffres décimaux de
la factorielle et le nombre de chiffres décimaux de ![]() :
:
def fact(n):
f = 1
a = n
while a > 0:
f *= a
a -= 1
return f
def nbChiffres(n):
if n == 0:
return 1
c = 0
a = n
while a > 0:
c += 1
a //= 10
return c
La fonction suivante affiche, parmi les entiers positifs inférieurs ou égaux à maxi, ceux qui sont égaux au nombre de chiffres de leur factorielle :
def cherche(maxi):
for i in range(maxi + 1):
if i == nbChiffres(fact(i)):
print(i)
return
On obtient :
>>> cherche (100) 1 22 23 24
Par ailleurs, on sait que pour tout ![]() le nombre de chiffres décimaux de
le nombre de chiffres décimaux de ![]() est :
est :
![]()
et que
Une condition suffisante pour que ![]() est donc :
est donc :
![]()
Or, en posant
![]()
on constate que :
![]()
La suite
![]()
![]()

Calculons le quotient de deux termes consécutifs :
![Rendered by QuickLaTeX.com \[\frac{u_{n+1}}{u_{n}}=\frac{a^{n+1}}{\left(\left(n+1\right)!\right)^{b}}\:\frac{\left(n!\right)^{b}}{a^{n}}=\frac{a}{\left(n+1\right)^{b}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-71cd88780823bcc8bbcb0bc8493074e6_l3.png)
Il apparaît que :
![]()
et, en particulier, qu’il existe
![]()
La suite
![]()
que
Bref, on a montré que :
![Rendered by QuickLaTeX.com \[\boxed{\forall\left(a,b\right)\in\left]0,+\infty\right[^{2},\:\lim_{n\rightarrow\infty}\frac{a^{n}}{\left(n!\right)^{b}}=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-10ece3dff3173d95290b1ede768b3a3b_l3.png)

Posons, pour tout ![]() :
:
![]()
![]()
![]()
![]()
Autre point de vue, utilisant le développement en série entière de l’exponentielle, ainsi que la formule du binôme :
![Rendered by QuickLaTeX.com \[n!e^{n}\geqslant\sum_{k=0}^{n}n!\frac{n^{k}}{k!}\geqslant\sum_{k=0}^{n}\binom{n}{k}n^{k}=\left(n+1\right)^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5a230284cf6d0334c2ff1a9a1eb3d9be_l3.png)

L’intégrale est « doublement impropre » : elle présente une singularité en 0 et une autre en ![]()
Pour la borne 0, on utilise l’équivalent :
![]()
Pour la borne ![]() on observe (avec la propriété des croissances comparées) que :
on observe (avec la propriété des croissances comparées) que :
![]()
![]()
Maintenant, fixons ![]() et choisissons des bornes
et choisissons des bornes ![]() et
et ![]() vérifiant
vérifiant ![]() En intégrant par parties, on obtient :
En intégrant par parties, on obtient :
![]()
Après passage à la limite (lorsque ![]() et
et ![]() :
:
![]()
![]()
![]()
On reconnaît aussitôt la factorielle :
![Rendered by QuickLaTeX.com \[\boxed{\forall n\in\mathbb{N},\thinspace\int_{0}^{+\infty}t^{n}e^{-t}\thinspace dt=n!}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-df2cbc7c1bb09a320ebd75da26d45fe0_l3.png)
Remarque
Notre fonction ![]() est une translatée de la fonction Gamma d’Euler, officiellement définie par :
est une translatée de la fonction Gamma d’Euler, officiellement définie par :
![]()
Pour en savoir plus à ce sujet, voir par exemple ici.
Soit ![]() un quadruplet solution. Alors
un quadruplet solution. Alors ![]() donc
donc ![]() c’est-à-dire
c’est-à-dire ![]() De même pour
De même pour ![]() et
et ![]() et donc :
et donc :
![]()
ou encore
On essaie maintenant toutes ces possibilités. Vue la symétrie des rôles de ![]() et puisque
et puisque ![]() il suffit de tester successivement :
il suffit de tester successivement :
On ne trouve au final qu’une seule solution :
![]()

Notons ![]() le sous-ensemble de
le sous-ensemble de ![]() constitué des produits de factorielles de nombres premiers et des quotients de tels produits.
constitué des produits de factorielles de nombres premiers et des quotients de tels produits.
Il est clair que ![]() (considérer le produit vide ou bien, tout simplement :
(considérer le produit vide ou bien, tout simplement : ![]()
Par définition, ![]() est stable par produit et par quotient.
est stable par produit et par quotient.
Montrons que ![]() D’évidence
D’évidence ![]() donc
donc ![]() Supposons (hypothèse de récurrence forte) que
Supposons (hypothèse de récurrence forte) que ![]() contienne tous les nombres premiers inférieurs ou égaux à
contienne tous les nombres premiers inférieurs ou égaux à ![]() pour un certain
pour un certain ![]() Soit
Soit ![]() le plus petit nombre premier supérieur à
le plus petit nombre premier supérieur à ![]() Comme :
Comme :
![]()
et vu que :
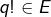
- tout
 est un produit de nombres premiers
est un produit de nombres premiers 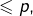 qui eux-mêmes appartiennent à
qui eux-mêmes appartiennent à 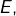
on constate que ![]()
Maintenant que l’inclusion ![]() est établie, et vu que tout entier
est établie, et vu que tout entier ![]() est produit de nombres premiers, on voit que
est produit de nombres premiers, on voit que ![]() et finalement (stabilité de
et finalement (stabilité de ![]() par quotient) que
par quotient) que ![]()

Soit ![]() Notons :
Notons :
![]()
et effectuons la chaîne de divisions euclidiennes :
![Rendered by QuickLaTeX.com \[\begin{array}{ccccc}A & = & a_{n}\thinspace n!+r_{n} & \text{avec} & 0\leqslant r_{n}<n!\\r_{n} & = & a_{n-1}\left(n-1\right)!+r_{n-1} & \text{avec} & 0\leqslant r_{n-1}<\left(n-1\right)!\\& \vdots & & \vdots\\r_{3} & = & a_{2}2!+r_{2} & \text{avec} & 0\leqslant r_{2}<2\\r_{2} & = & a_{1}1!+r_{1} & \text{avec} & 0\leqslant r_{1}<1\end{array}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-421fbce3e40cf70db31f7e3e9f58a06a_l3.png)
Visiblement
En outre, en convenant que ![]() désigne
désigne ![]() on voit que pour tout
on voit que pour tout ![]() :
:
![]()
ce qui impose ![]() c’est-à-dire :
c’est-à-dire :
![]()
En sommant toutes les égalités obtenues, on obtient :
![Rendered by QuickLaTeX.com \[A=\sum_{k=1}^{n}a_{k}\thinspace k!\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-644374c5e0e8c5b1561b07371e8e7014_l3.png)
En outre, si ![]() alors
alors ![]() d’après la toute première égalité, ce qui est absurde. Donc
d’après la toute première égalité, ce qui est absurde. Donc ![]() et l’existence est établie. Passons à l’unicité.
et l’existence est établie. Passons à l’unicité.
Supposons que ![]() et que
et que ![]() et
et ![]() vérifient :
vérifient :
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{m}a_{k}\thinspace k!=\sum_{k=1}^{n}b_{k}\thinspace k!\qquad\left(\diamondsuit\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f86d82e0a2f042e3e4c939c1f8788644_l3.png)
avec en outre :
![]()
Déjà, il est nécessaire qu’on ait ![]() En effet, si par exemple
En effet, si par exemple ![]() alors :
alors :
![Rendered by QuickLaTeX.com \[ \sum_{k=1}^{m}a_{k}\thinspace k!\leqslant\sum_{k=1}^{m}k\thinspace k!=\left(m+1\right)!-1 \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-09019cef7d8a4ab416f343d9daa06a49_l3.png)
![Rendered by QuickLaTeX.com \[ \sum_{k=1}^{n}b_{k}\thinspace k!\geqslant b_{n}\thinspace n!\geqslant n!>m!\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2428fcc355d29ce389971611339dffd2_l3.png)
ce qui contredit
![]()
Si par exemple ![]() alors d’une part :
alors d’une part :
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{s}a_{k}\thinspace k!\leqslant a_{s}\thinspace s!+s!-1=\left(a_{s}+1\right)s!-1\leqslant b_{s}\thinspace s!-1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cf8c3ec195abb7356ebcd33e7f48be89_l3.png)
et d’autre part :
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{s}b_{k}\thinspace k!\geqslant b_{s}\thinspace s!\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bca8c398fb8af41ff4ba211511520989_l3.png)
ce qui contredit le fait que :
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{s}a_{k}\thinspace k!=\sum_{k=1}^{s}b_{k}\thinspace k!\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b9e2d9f480b9b03952bffbf8d0255dd3_l3.png)
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
