

De toute évidence :
![]()
Pour
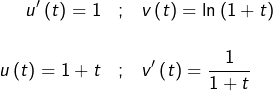
(noter la petite astuce pour le choix d’une primitive de
![]()
![]()
Pour
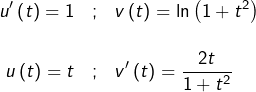
On obtient ainsi :
![]()
![]()
![]()
![]()

On effectue une première intégration par parties en posant :
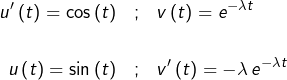
ce qui donne :
![]()
On pose donc :
![]()
de sorte que
![]()
et l’on intègre par parties posant :
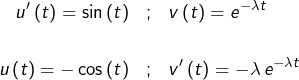
pour obtenir :
![]()
c’est-à-dire :
![]()
La combinaison des relations ![]() et
et ![]() donne :
donne :
![]()
![Rendered by QuickLaTeX.com \[ \boxed{A_{\lambda}=\frac{\lambda}{1+\lambda^{2}}\thinspace e^{-\lambda\pi}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a3ce9ea9e41605e34988355c61d3073d_l3.png)
![]()
Pour retrouver ceci directement (ie : sans calculer ![]() au préalable), il suffit d’observer que :
au préalable), il suffit d’observer que :
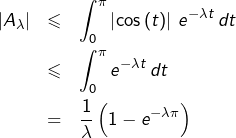
On voit alors que, pour tout
![]()
d’où
Le théorème de décomposition d’une fraction rationnelle à coefficients réels donne, a priori, l’existence d’un unique triplet ![]() tel que :
tel que :
![]()
Après réduction au même dénominateur, il vient :
![]()
Noter qu’a priori, l’égalité ne vaut que si ![]() mais elle est aussi vraie pour
mais elle est aussi vraie pour ![]() par continuité !
par continuité !

Par identification (même si ce n’est pas la méthode la plus efficace…), on parvient au système :
![Rendered by QuickLaTeX.com \[ \left\{ \begin{array}{ccc} a+b & = & 0\\ -a+b+c & = & 0\\ a+c & = & 1 \end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-290f4b870ffa71778d088595fdd50a89_l3.png)
d’où facilement :
![]()
Ainsi, l’intégrale à calculer s’écrit :
![]()
Posons temporairement :
![]()
et mettons le trinôme au dénominateur sous forme canonique :
![Rendered by QuickLaTeX.com \[ B=\int_{0}^{1}\frac{-t+2}{\left(t-\frac{1}{2}\right)^{2}+\frac{3}{4}}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-725ea4acf8f79de3b74e1f800a0aa542_l3.png)
Si l’on pose maintenant ![]() il vient :
il vient :
![Rendered by QuickLaTeX.com \[ B=\int_{-1/2}^{1/2}\frac{\frac{3}{2}-u}{u^{2}+\frac{3}{4}}\thinspace du\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4c0e59ed8a27537ee8f4984ad511611c_l3.png)
c’est-à-dire :
![Rendered by QuickLaTeX.com \[ B=\frac{3}{2}\int_{-1/2}^{1/2}\thinspace\frac{du}{u^{2}+\frac{3}{4}}-\int_{-1/2}^{1/2}\thinspace\frac{u}{u^{2}+\frac{3}{4}}\thinspace du\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0413757ba77d4cc0b43131d1cd0332a6_l3.png)
On voit ainsi que :
![Rendered by QuickLaTeX.com \[ B=\frac{3}{2}\left[\frac{2}{\sqrt{3}}\arctan\left(\frac{2u}{\sqrt{3}}\right)\right]_{-1/2}^{1/2}-\left[\frac{1}{2}\ln\left(u^{2}+\frac{3}{4}\right)\right]_{-1/2}^{1/2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6bc9f08955df74e141785ee8a8a81ec3_l3.png)
c’est-à-dire :
![]()
En reportant ceci dans ![]() , on conclut que :
, on conclut que :
![Rendered by QuickLaTeX.com \[ \boxed{\int_{0}^{1}\frac{dt}{1+t^{3}}=\frac{\pi\sqrt{3}}{9}+\frac{1}{3}\ln\left(2\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-eae447ae406ae32c20317379395da1e7_l3.png)

Comme le suggère l’indication, on va utiliser la majoration classique :
![]()
Noter que cette inégalité peut être vue comme une conséquence de la concavité de la fonction logarithme (le graphe de ![]() est « en-dessous » de chacune de ses tangentes et, notamment, en-dessous de sa tangente à l’origine, qui a pour équation
est « en-dessous » de chacune de ses tangentes et, notamment, en-dessous de sa tangente à l’origine, qui a pour équation ![]()
Bref, on voit par croissance de l’intégrale que, pour tout ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[ \boxed{\lim_{n\rightarrow\infty}\int_{0}^{1}\ln\left(1+t^{n}\right)\thinspace dt=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-71f579d2fc7029e82e10ca5efeb08e74_l3.png)

Effectuons le changement de variable ![]() dans l’intégrale qui définit
dans l’intégrale qui définit ![]()
On obtient :
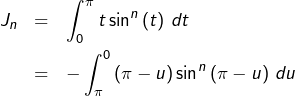
Mais ![]() pour tout
pour tout ![]() et donc :
et donc :
![]()
c’est-à-dire, en séparant cette dernière intégrale en deux :
![]()
ou encore :
![]()
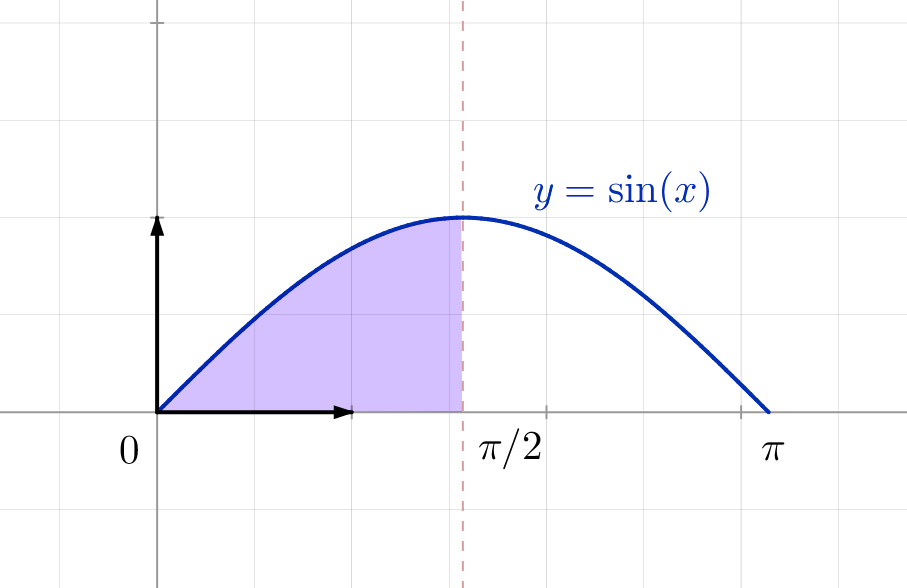
Pour finir, on voit avec la relation de Chasles que :
![Rendered by QuickLaTeX.com \[\int_{0}^{\pi}\sin^{n}\left(u\right)\thinspace du = \int_{0}^{\pi/2}\sin^{n}\left(u\right)\thinspace du+\int_{\pi/2}^{\pi}\sin^{n}\left(u\right)\thinspace du\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-32be3a946a456ba11b5eea700522d106_l3.png)
et si l’on pose
![Rendered by QuickLaTeX.com \[ \int_{\pi/2}^{\pi}\sin^{n}\left(u\right)\thinspace du=-\int_{\pi/2}^{0}\sin^{n}\left(\pi-v\right)\thinspace dv=\int_{0}^{\pi/2}\sin^{n}\left(u\right)\thinspace du\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6daf28cd99182a98ab2edc4fded43d5b_l3.png)
![]()
Finalement :
![]()

Montrons que :
![Rendered by QuickLaTeX.com \[\boxed{\lim_{x\rightarrow0^{+}}\frac{1}{x}\int_{0}^{x}f\left(t\right)\thinspace dt=f\left(0\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-29fe247e68f49ab0246c4d0eea6c9649_l3.png)
ou bien, ce qui revient au même, que :
![]()
Pour cela, fixons un réel
![]()
Il en résulte que pour tout
![]()
et donc, après division par
![]()

On observe que, pour tout ![]() :
:
![]()
Montrons donc que :
![Rendered by QuickLaTeX.com \[\boxed{\lim_{x\rightarrow0^{+}}\int_{x}^{2x}\frac{\cos\left(t\right)}{t}\thinspace dt=\ln\left(2\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9068a3279abe0df1a5af006fabcf268d_l3.png)
Pour cela, écrivons la différence de manière plus homogène. En profitant de l’observation ci-dessus, on voit que pour tout ![]() :
:
![]()
Voyons deux manières de conclure que cette dernière quantité tend vers ![]() lorsque
lorsque ![]()
La première méthode est pragmatique (on va profiter de la forme particulière de l’expression ci-dessus) tandis que la seconde est plus abstraite mais aussi plus générale (elle pourrait s’appliquer, pratiquement sans aucune modification, à une vaste gamme d’exemple similaires).
➢ Méthode 1
On écrit, artificiellement, que pour tout ![]() :
:
![]()
Il en résulte que, pour tout ![]() :
:
![]()
![]()
➢ Méthode 2
On utilise le :
Lemme
Soient ![]() un intervalle et
un intervalle et ![]() une application continue et bornée.
une application continue et bornée.
Soient ![]() un intervalle,
un intervalle, ![]() et
et ![]() deux applications telles que :
deux applications telles que :
![]()
![Rendered by QuickLaTeX.com \[\lim_{x\rightarrow x_{0}}\int_{\alpha\left(x\right)}^{\beta\left(x\right)}f\left(t\right)\thinspace dt=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a14931408386aeab5905060810b2603b_l3.png)
On peut retenir ce lemme sous la forme suivante :
Sur un intervalle dont la longueur tend vers 0, l’intégrale d’une quantité bornée tend vers 0.
La preuve est immédiate. Si ![]() est un majorant de
est un majorant de ![]() pour
pour ![]() alors :
alors :
![Rendered by QuickLaTeX.com \[ \forall x\in J,\thinspace\left|\int_{\alpha\left(x\right)}^{\beta\left(x\right)}f\left(t\right)\thinspace dt\right|\leqslant M\left|\alpha\left(x\right)-\beta\left(x\right)\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e70c5c1c6e8a6cb1ee23e2399f133518_l3.png)
Ce lemme s’applique à l’exemple proposé puisque l’application ![]() est prolongeable par continuité en 0 et donc bornée au voisinage à droite de 0.
est prolongeable par continuité en 0 et donc bornée au voisinage à droite de 0.
Si ![]() est solution de l’équation proposée, la relation :
est solution de l’équation proposée, la relation :
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}f'\left(x\right) & = & -\left[\int_{0}^{x}\,f\left(t\right)\,dt+x\,f\left(x\right)\right]+x\,f\left(x\right)\\& = & -\int_{0}^{x}\,f\left(t\right)\,dt\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-8aedb89b5700ba92bb156319694bdcbc_l3.png)
Ainsi ![]() est de classe
est de classe ![]() et :
et :
![]()
On sait alors qu’il existe des réels ![]() tels que
tels que ![]()
Réciproquement, il s’agit de savoir quelles sont les fonctions de ce type qui conviennent. On calcule, en intégrant par parties :
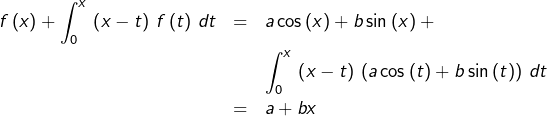
La famille ![]() étant libre, la condition imposée à
étant libre, la condition imposée à ![]() équivaut à
équivaut à ![]()
Finalement, la seule solution continue de l’équation proposée est ![]()

En posant ![]() on obtient :
on obtient :
![]()
Notons dans la suite :
![]()
On observe que :
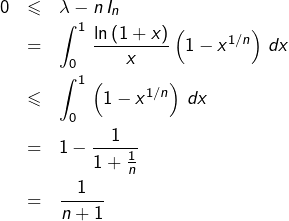
d’où il résulte que :
![]()
Pour finir, on peut exprimer ![]() comme la somme d’une série convergente. En effet :
comme la somme d’une série convergente. En effet :
![Rendered by QuickLaTeX.com \[ \lambda=\int_{0}^{1}\,\left(\sum_{n=1}^{\infty}\,\frac{\left(-1\right)^{n-1}}{n}x^{n-1}\right)\,dx\underset{\star}{=}\sum_{n=1}^{\infty}\,\frac{\left(-1\right)^{n-1}}{n^{2}}\underset{\star\star}{=}\frac{\pi^{2}}{12}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0980300fafc09cad867ebfbd8643f330_l3.png)
Pour l’égalité ![]() il suffit de prouver que :
il suffit de prouver que :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}\int_{0}^{1}\left(\sum_{k=n}^{\infty}\frac{\left(-1\right)^{k-1}}{k}x^{k-1}\right)\thinspace dx=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3ad9973acfe7b21cd411c142d660e23b_l3.png)
![Rendered by QuickLaTeX.com \[ \forall x\in\left]0,1\right[,\thinspace\forall n\geqslant2,\thinspace\left|\sum_{k=n}^{\infty}\left(-1\right)^{k-1}\thinspace\frac{x^{k-1}}{k}\right|\leqslant\frac{x^{n-1}}{n-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ae32de66af8e9847540879c7af1cdf2b_l3.png)
![Rendered by QuickLaTeX.com \[ \left|\int_{0}^{1}\left(\sum_{k=n}^{\infty}\frac{\left(-1\right)^{k-1}}{k}x^{k-1}\right)\thinspace dx\right|\leqslant\int_{0}^{1}\frac{x^{n-1}}{n-1}\thinspace dx=\frac{1}{n\left(n-1\right)}\underset{n\rightarrow\infty}{\rightarrow}0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3570e8b8a3fd41d1f1522d12aa15e44b_l3.png)
Quant à la relation ![]() elle découle de la formule classique :
elle découle de la formule classique :
![Rendered by QuickLaTeX.com \[\boxed{\sum_{n=1}^{\infty}\frac{1}{n^{2}}=\frac{\pi^{2}}{6}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f6d02d8d4dd7262b95c08fde74347572_l3.png)
![Rendered by QuickLaTeX.com \[ \sum_{n=1}^{\infty}\frac{1}{n^{2}}-\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n-1}}{n^{2}}=\sum_{n=1}^{\infty}\frac{1+\left(-1\right)^{n}}{n^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1effa63e489b5cd97554535dcbcb2c33_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{\pi^{2}}{6}-\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n-1}}{n^{2}}=\sum_{p=1}^{\infty}\frac{2}{\left(2p\right)^{2}}=\frac{1}{2}\sum_{p=1}^{\infty}\frac{1}{p^{2}}=\frac{\pi^{2}}{12}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2e4c95b476cc65f79fa76d830f766861_l3.png)
En conclusion :
![Rendered by QuickLaTeX.com \[\boxed{\int_0^1\ln\left(1+t^n\right)\,dt\sim\frac{\pi^2}{12n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a08cf262641fa159addbe1e680755051_l3.png)
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
