Solutions détaillées de neuf exercices sur la notion d’application (fiche 02).
Cliquer ici pour accéder aux énoncés.


Notons :
![]()
![]()
➭ Si ![]() alors
alors ![]() s’annule deux fois en changeant de signe et l’on voit que
s’annule deux fois en changeant de signe et l’on voit que ![]() présente un maximum local
présente un maximum local ![]() et un minimum local
et un minimum local ![]() , ce qui prouve sa non-injectivité.
, ce qui prouve sa non-injectivité.
Afin d’être totalement explicite sur ce point, on peut montrer que certains réels ont trois antécédents (détail ci-dessous).
Détail (cliquer pour déplier / replier)
Le graphe de ![]() présente une inflexion au point d’abscisse
présente une inflexion au point d’abscisse ![]() .
.
L’ordonnée correspondante est :
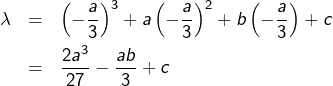
On vérifie l’équation
![]()
![]()
![]()
On a donc bien trois solutions pour l’équation ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{-\frac a3-\frac{\sqrt{3\Delta'}}3,\qquad-\frac a3,\qquad-\frac a3+\frac{\sqrt{3\Delta'}}3}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fc2d645aa6ff4bff13c3d5b058111747_l3.png)
➭ En revanche, si ![]() alors
alors ![]() est positive (et s’annule au maximum une fois) d’où la stricte croissance de
est positive (et s’annule au maximum une fois) d’où la stricte croissance de ![]() et donc son injectivité.
et donc son injectivité.
En outre ![]() est surjective d’après le théorème des valeurs intermédiaires, puisque
est surjective d’après le théorème des valeurs intermédiaires, puisque ![]() et
et ![]() Finalement :
Finalement :
![]()

Supposons ![]() croissante (notons qu’il s’agit d’une croissance stricte en raison de l’injectivité de
croissante (notons qu’il s’agit d’une croissance stricte en raison de l’injectivité de ![]()
Soient ![]() tels que
tels que ![]() . Comme
. Comme ![]() est injective, alors
est injective, alors ![]() .
.
Si ![]() alors
alors ![]() par croissance stricte de
par croissance stricte de ![]() , c’est-à-dire
, c’est-à-dire ![]() : c’est absurde ! Donc
: c’est absurde ! Donc ![]()
Ceci prouve la stricte croissance de ![]() .
.
Supposons maintenant ![]() impaire et soit
impaire et soit ![]() On observe que :
On observe que :
![]()

Notons ![]() l’ensemble des injections de
l’ensemble des injections de ![]() dans E.
dans E.
Afin de dénombrer ![]() , posons
, posons ![]() et notons
et notons ![]() l’ensemble des injections de
l’ensemble des injections de ![]() dans E qui envoient 0 sur
dans E qui envoient 0 sur ![]() (ceci pour chaque
(ceci pour chaque ![]()
On observe que ![]() est l’union disjointe des
est l’union disjointe des ![]() pour
pour ![]() et, de plus, que
et, de plus, que ![]() pour tout
pour tout ![]() Par conséquent :
Par conséquent :
![]()
Notons maintenant ![]() l’ensemble des surjections de E dans
l’ensemble des surjections de E dans ![]() .
.
L’observation-clef est la suivante : parmi les applications de E dans ![]() , deux seulement sont non-surjectives. Ce sont les applications constantes : l’une envoie tout élément de E sur 0 et l’autre envoie tout élément de E sur 1. Or il existe
, deux seulement sont non-surjectives. Ce sont les applications constantes : l’une envoie tout élément de E sur 0 et l’autre envoie tout élément de E sur 1. Or il existe ![]() applications de E dans
applications de E dans ![]() et donc :
et donc :
![]()

Distinguons deux cas de figure.
➭ Si ![]() est fini, cette affirmation est correcte. En effet, si l’on note
est fini, cette affirmation est correcte. En effet, si l’on note ![]() et
et ![]() (avec
(avec ![]() , alors l’existence d’une injection
, alors l’existence d’une injection ![]() impose
impose ![]() et donc
et donc ![]() (et au passage
(et au passage ![]() Or une injection d’un ensemble fini dans un ensemble de même cardinal est nécessairement bijective.
Or une injection d’un ensemble fini dans un ensemble de même cardinal est nécessairement bijective.
➭ La situation est différente si ![]() est infini. Par exemple, (en notant
est infini. Par exemple, (en notant ![]() l’ensemble des entiers naturels pairs) : l’application
l’ensemble des entiers naturels pairs) : l’application ![]() est une injection non surjective de
est une injection non surjective de ![]() dans l’une de ses parties.
dans l’une de ses parties.

Soient ![]() et
et ![]() dans
dans ![]() tels que :
tels que : ![]()
En passant aux modules : ![]() Donc
Donc ![]() c’est-à-dire
c’est-à-dire ![]() et donc
et donc ![]() Mais comme
Mais comme ![]() ce impose
ce impose ![]() L’injectivité de
L’injectivité de ![]() est établie.
est établie.
Par ailleurs, si ![]() alors en notant
alors en notant ![]() (avec
(avec ![]() réels non tous deux nuls) et
réels non tous deux nuls) et ![]() on a
on a ![]() . Comme
. Comme
![]()
![]()
Finalement :
![]()
Ainsi, ![]() est surjective et donc bijective.
est surjective et donc bijective.
Sa bijection réciproque est :
![]()
Ensuite :
![Rendered by QuickLaTeX.com f\left\langle \left]0,+\infty\right[\times\left\{ \frac{\pi}{2}\right\} \right\rangle =i\left]0,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-a2006ec4068bd52ec5d2ba7c9181d920_l3.png) : demi-axe imaginaire positif (ouvert)
: demi-axe imaginaire positif (ouvert)![Rendered by QuickLaTeX.com f\left\langle \left\{ 1\right\} \times\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\right\rangle =\left\{ e^{i\theta};\thinspace\theta\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\right\}](https://math-os.com/wp-content/ql-cache/quicklatex.com-3c4d26955919f995c1ccf8889a92ac4d_l3.png) : demi-cercle unité (abscisses
: demi-cercle unité (abscisses 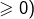
![Rendered by QuickLaTeX.com f\left\langle \left[1,2\right]\times\left]-\pi,\pi\right]\right\rangle](https://math-os.com/wp-content/ql-cache/quicklatex.com-9ecbc5141acbae834e196af65d22f075_l3.png) : couronne fermée, centrée en 0, de rayons 1 et 2.
: couronne fermée, centrée en 0, de rayons 1 et 2.
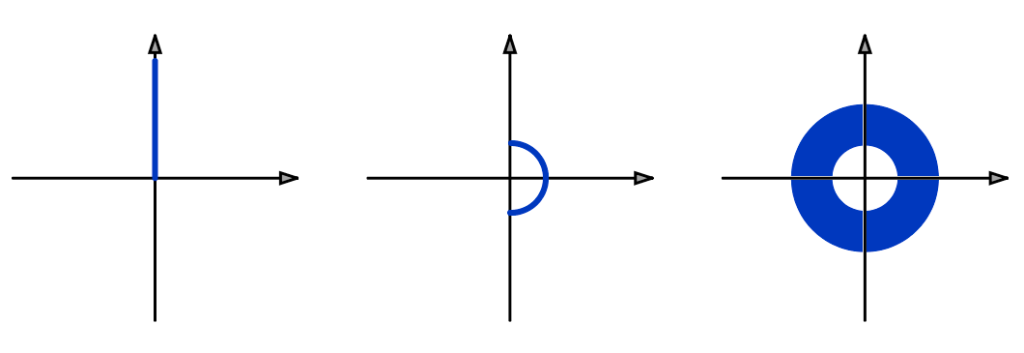

Soient ![]() tels que
tels que ![]() c’est-à-dire :
c’est-à-dire :
![]()
![]()
L’injectivité de ![]() est établie.
est établie.
Soit maintenant ![]() Si
Si ![]() est un antécédent de
est un antécédent de ![]() par
par ![]() alors :
alors :
![]()
![]()
![]()
![]()
![]()
Finalement, l’application ![]() induit une bijection
induit une bijection
![]()
![Rendered by QuickLaTeX.com \[\boxed{\Phi^{-1}:\mathbb{C}-\mathbb{U}\rightarrow\mathbb{C};\thinspace w\mapsto\frac{w}{1-\left|w\right|}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5ac748ff01d76e4987cfc5869d361cc9_l3.png)

Soient ![]() tels que
tels que ![]() Alors :
Alors :
![]()
Etant donné ![]() l’équation
l’équation ![]() d’inconnue
d’inconnue ![]() équivaut à :
équivaut à :
![]()
En revanche, ![]() ne possède aucun antécédent (et donc
ne possède aucun antécédent (et donc ![]() n’est pas surjective).
n’est pas surjective).
Montrons maintenant que si ![]() alors
alors ![]()
Etant donné ![]() on peut poser :
on peut poser : ![]() avec
avec ![]() et
et ![]() Alors :
Alors :
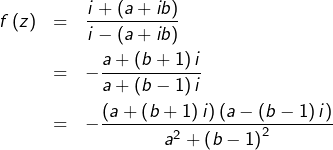
![]()
![]()
Soit ![]() avec
avec ![]() Comme
Comme ![]() on sait qu’il existe
on sait qu’il existe ![]() tel que
tel que ![]() il reste à vérifier que
il reste à vérifier que ![]() Or :
Or :
![]()
En conclusion, ![]() induit une bijection de
induit une bijection de ![]() sur
sur ![]() dont la bijection réciproque est :
dont la bijection réciproque est :
![]()
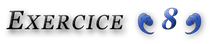
L’application
![]()
![]()
Ceci prouve que la restriction de ![]() à
à ![]() est strictement croissante (donc injective).
est strictement croissante (donc injective).
Comme ![]() et vu que
et vu que ![]() alors (TVI) :
alors (TVI) : ![]()
Ainsi ![]() induit une bijection
induit une bijection ![]() de
de ![]() sur
sur ![]() .
.
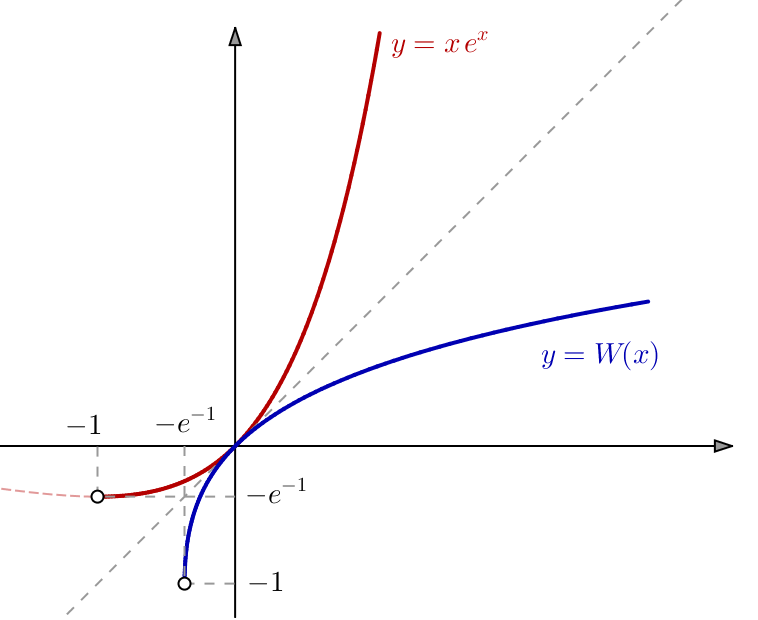
Notons ![]() Comme
Comme ![]() alors
alors ![]() Ensuite, comme
Ensuite, comme ![]() on voit que
on voit que
![]()
D’après la formule de Taylor-Young au premier ordre :
![]()
![]()
Par ailleurs, pour tout ![]() :
:
![]()
![]()
![]()
![]()

Soit ![]() une suite injective à termes dans
une suite injective à termes dans ![]() telle que
telle que ![]() .
.
On peut considérer l’application :
![Rendered by QuickLaTeX.com \[f:\left[0,1\right]\rightarrow\left[0,1\right[,\thinspace x\mapsto\left\{ \begin{array}{cc}u_{n+1} & \text{s'il existe }n\in\mathbb{N}\text{ tel que }x=u_{n}\\\\x & \text{sinon}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6dd124cfa35f50899709e5aa81f400a4_l3.png)
- ou bien il existe
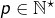 tel que
tel que 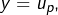 auquel cas
auquel cas 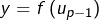
- ou bien
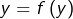
![]() est injective car :
est injective car :
- sa restriction
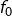 à
à 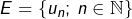 est injective
est injective - sa restriction
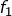 à
à ![Rendered by QuickLaTeX.com \left[0,1\right]-E](https://math-os.com/wp-content/ql-cache/quicklatex.com-ee4918329b1b69a42c384efcaabd3a89_l3.png) est injective
est injective ![Rendered by QuickLaTeX.com f_{0}\left\langle E\right\rangle \cap f_{1}\left\langle \left[0,1\right]-E\right\rangle =\emptyset](https://math-os.com/wp-content/ql-cache/quicklatex.com-6eb2ebe3058ccd1c61a10013daa835d1_l3.png)
Par exemple, on peut choisir la suite ![]() ce qui donne la bijection :
ce qui donne la bijection :
![Rendered by QuickLaTeX.com \[\boxed{f:\left[0,1\right]\rightarrow\left[0,1\right[,\thinspace x\mapsto\left\{ \begin{array}{cc}2^{-n-1} & \text{s'il existe }n\in\mathbb{N}\text{ tel que }x=2^{-n}\\\\x & \text{sinon}\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-04ab8bb909319fc49822470241e89d4d_l3.png)
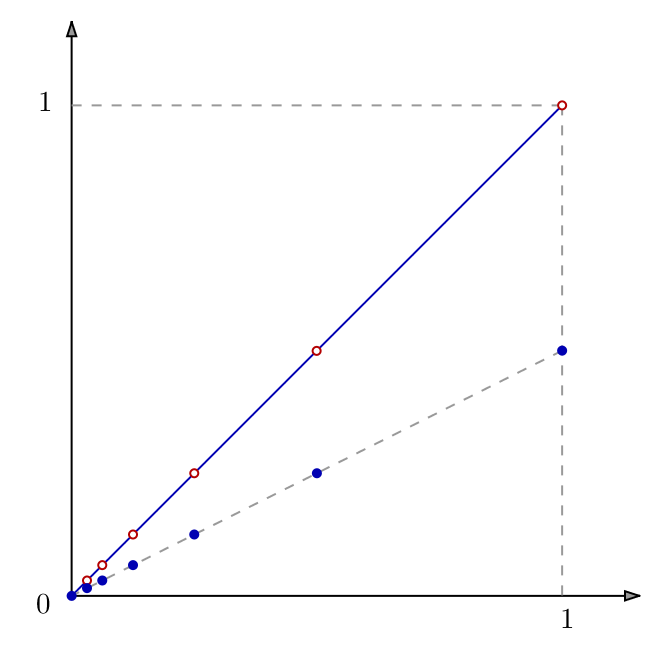
Un disque bleu indique que le point en question appartient au graphe de ![]()
Un cercle rouge indique que le point en question n’appartient pas au graphe de ![]()
D’une manière générale, si ![]() est une bijection, alors
est une bijection, alors ![]() ne peut pas être continue car sinon
ne peut pas être continue car sinon ![]() serait un segment.
serait un segment.
Elle ne peut pas non plus être monotone, car étant donnés deux intervalles ![]() non triviaux, toute bijection monotone
non triviaux, toute bijection monotone ![]() est continue. Ceci résulte du théorème de la limite monotone :
est continue. Ceci résulte du théorème de la limite monotone : ![]() admet, en tout point intérieur à
admet, en tout point intérieur à ![]() une limite à gauche et une limite à droites toutes deux finies. Si ces limites étaient distinctes, on aurait un « trou » dans
une limite à gauche et une limite à droites toutes deux finies. Si ces limites étaient distinctes, on aurait un « trou » dans ![]() ce qui est impossible vu que
ce qui est impossible vu que ![]() est un intervalle. Argument similaire pour une extrémité éventuelle de
est un intervalle. Argument similaire pour une extrémité éventuelle de ![]()
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
