Solution pour le challenge 87
Commençons par deux petites observations :
1 – Si 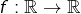 est telle que
est telle que 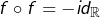 alors
alors  est une bijection. On sait en effet que :
est une bijection. On sait en effet que :
- si
 est injective, alors
est injective, alors  est injective,
est injective,
- si
 est surjective, alors
est surjective, alors  est surjective.
est surjective.
2 – Si 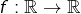 est telle que
est telle que 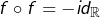 alors
alors  est nécessairement discontinue. En effet, si
est nécessairement discontinue. En effet, si  était continue,
était continue,  serait strictement monotone en raison de son injectivité (voir cet article) et, par conséquent,
serait strictement monotone en raison de son injectivité (voir cet article) et, par conséquent, 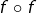 serait strictement croissante, ce qui est absurde (puisque
serait strictement croissante, ce qui est absurde (puisque 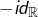 n’a pas cette propriété).
n’a pas cette propriété).
Cela dit, soit 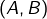 une partition de
une partition de ![Rendered by QuickLaTeX.com \left]0,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-90d2d03eec9a031b0d2601b2f615f2df_l3.png) en parties équipotentes (toutes deux non dénombrables) et soit
en parties équipotentes (toutes deux non dénombrables) et soit 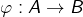 une bijection. Pour tout
une bijection. Pour tout 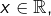 posons :
posons :
![Rendered by QuickLaTeX.com \[f\left(x\right)=\left\{ \begin{array}{cc}0 & \text{si }x=0\\\varphi\left(x\right) & \text{si }x\in A\\-\varphi\left(-x\right) & \text{si }x\in-A\\-\varphi^{-1}\left(x\right) & \text{si }x\in B\\\varphi^{-1}\left(-x\right) & \text{si }x\in-B\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c70790a2c6b36822e607c210c335d97b_l3.png)
où
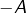
désigne l’ensemble des opposés des éléments de
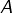
(et notation analogue pour
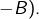
On constate alors que 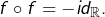 On vérifie cette égalité en se donnant
On vérifie cette égalité en se donnant 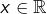 et en envisageant différents cas, selon que
et en envisageant différents cas, selon que 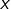 appartient à
appartient à 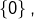
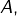
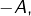
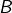 ou
ou 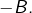 Par exemple, si
Par exemple, si 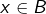 alors
alors 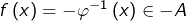 et donc :
et donc :
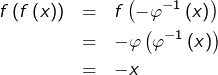
Choissisons de partitionner ![Rendered by QuickLaTeX.com \left]0,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-90d2d03eec9a031b0d2601b2f615f2df_l3.png) comme ceci :
comme ceci :
![Rendered by QuickLaTeX.com \[A=\bigcup_{k=0}^{\infty}\left]2k,2k+1\right],\qquad B=\bigcup_{k=0}^{\infty}\left]2k+1,2k+2\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ea064b8628ecf439755b2522b1f0eb2d_l3.png)
Autrement dit :
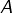
(resp.
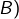
est l’ensemble des réels strictement positifs dont la partie entière par excès est impaire (resp. paire). Considérons la bijection :
![Rendered by QuickLaTeX.com \[\varphi:A\rightarrow B,\thinspace x\mapsto x+1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a1f38e219bcc40ed505a10e7519e77ea_l3.png)
et posons, pour tout
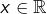
:
![Rendered by QuickLaTeX.com \[f\left(x\right)=\left\{ \begin{array}{cc}0 & \text{si }x=0\\x+1 & \text{si }x\in A\\x-1 & \text{si }x\in-A\\-x+1 & \text{si }x\in B\\-x-1 & \text{si }x\in-B\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6e660390253b17e10e735f7db1e7bff3_l3.png)
Conformément aux explications précédentes,

est une anti-involution de
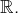
Voici à quoi ressemble son graphe (les petits disques rouges indiquent un point du graphe; en revanche, les points figurés par un petit cercle rouge n’en font pas partie) :
Remarque
En dimension paire, les difficultés disparaissent : l’application
![Rendered by QuickLaTeX.com \[\mathbb{C}^{n}\rightarrow\mathbb{C}^{n},\thinspace\left(z_{1},\cdots,z_{n}\right)\mapsto\left(iz_{1},\cdots,iz_{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fa0180ec364c04b230d73a1151e4545e_l3.png)
est une anti-involution.
Pour consulter l’énoncé, c’est ici
 est injective, alors
est injective, alors  est injective,
est injective, est surjective, alors
est surjective, alors  est surjective.
est surjective.![Rendered by QuickLaTeX.com \[f\left(x\right)=\left\{ \begin{array}{cc}0 & \text{si }x=0\\\varphi\left(x\right) & \text{si }x\in A\\-\varphi\left(-x\right) & \text{si }x\in-A\\-\varphi^{-1}\left(x\right) & \text{si }x\in B\\\varphi^{-1}\left(-x\right) & \text{si }x\in-B\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c70790a2c6b36822e607c210c335d97b_l3.png)
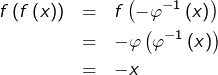
![Rendered by QuickLaTeX.com \[A=\bigcup_{k=0}^{\infty}\left]2k,2k+1\right],\qquad B=\bigcup_{k=0}^{\infty}\left]2k+1,2k+2\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ea064b8628ecf439755b2522b1f0eb2d_l3.png)
![]()
![Rendered by QuickLaTeX.com \[f\left(x\right)=\left\{ \begin{array}{cc}0 & \text{si }x=0\\x+1 & \text{si }x\in A\\x-1 & \text{si }x\in-A\\-x+1 & \text{si }x\in B\\-x-1 & \text{si }x\in-B\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6e660390253b17e10e735f7db1e7bff3_l3.png)
![]()
![Rendered by QuickLaTeX.com \[f\left(x\right)=\left\{ \begin{array}{cc}0 & \text{si }x=0\\\varphi\left(x\right) & \text{si }x\in A\\-\varphi\left(-x\right) & \text{si }x\in-A\\-\varphi^{-1}\left(x\right) & \text{si }x\in B\\\varphi^{-1}\left(-x\right) & \text{si }x\in-B\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c70790a2c6b36822e607c210c335d97b_l3.png)
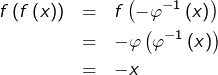
![Rendered by QuickLaTeX.com \[A=\bigcup_{k=0}^{\infty}\left]2k,2k+1\right],\qquad B=\bigcup_{k=0}^{\infty}\left]2k+1,2k+2\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ea064b8628ecf439755b2522b1f0eb2d_l3.png)
![]()
![Rendered by QuickLaTeX.com \[f\left(x\right)=\left\{ \begin{array}{cc}0 & \text{si }x=0\\x+1 & \text{si }x\in A\\x-1 & \text{si }x\in-A\\-x+1 & \text{si }x\in B\\-x-1 & \text{si }x\in-B\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6e660390253b17e10e735f7db1e7bff3_l3.png)
![]()