Solution pour le challenge 86
Avant toutes choses, révisons nos fondamentaux. Etant donné ![]() si l’on pose pour tout
si l’on pose pour tout ![]() :
:
![]()
- Pour tout
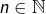 :
:
donc :![Rendered by QuickLaTeX.com \[10^{n}x-1<\left\lfloor 10^{n}x\right\rfloor \leqslant10^{n}x\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3e51bfdaaddd24e0425cbdd2ed130012_l3.png)
Ceci prouve, d’après le théorème d’encadrement, que![Rendered by QuickLaTeX.com \[x-10^{-n}<r_{n}\leqslant x\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4330a072ee95fa539c57429533e63b7d_l3.png)
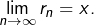
- D’après l’inégalité :
on a aussi :![Rendered by QuickLaTeX.com \[\left\lfloor 10^{n}x\right\rfloor \leqslant10^{n}x\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-50052ccee2f080e7ce76ec1f69e89915_l3.png)
donc :![Rendered by QuickLaTeX.com \[10\left\lfloor 10^{n}x\right\rfloor \leqslant10^{n+1}x\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-be5eb55ba70698bdf3320ab1f26c0ae9_l3.png)
et donc, après multiplication par![Rendered by QuickLaTeX.com \[10\left\lfloor 10^{n}x\right\rfloor \leqslant\left\lfloor 10^{n+1}x\right\rfloor\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d53a16e56d89ea1d77e7e60174fd0af4_l3.png)
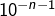 :
:
La suite![Rendered by QuickLaTeX.com \[r_{n}\leqslant r_{n+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-55ded53c9e84c6ac9f71f2fcce378f6f_l3.png)
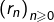 est donc bien croissante.
est donc bien croissante.
Maintenant considérons la suite de terme général :
![]()
![Rendered by QuickLaTeX.com \[\rho_{n}=\dfrac{s_{n+1}}{s_{n}}=\dfrac{n}{n+1}\thinspace\dfrac{\left\lfloor \dfrac{3n+3}{3}\right\rfloor }{\left\lfloor \dfrac{3n}{2}\right\rfloor }\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ded25492f0c6baa76ef3fa47305b45ba_l3.png)
![]()
![]()
Moralité : étant donné ![]() la suite
la suite ![]() converge vers
converge vers ![]() mais elle n’est pas croissante en général. Cela dit, son sens de variation n’est pas arbitraire puisque, pour tout
mais elle n’est pas croissante en général. Cela dit, son sens de variation n’est pas arbitraire puisque, pour tout ![]() la suite extraite
la suite extraite ![]() est croissante !
est croissante !
Pour consulter l’énoncé, c’est ici

