Solution pour le challenge 83
Solution 1 (proposée par Johann Fraleux)
Montrons d’abord que pour tous ![]() ,
, ![]() sont en progression géométrique.
sont en progression géométrique.
Le cas ![]() est évident et pour
est évident et pour ![]() , si l’on pose
, si l’on pose ![]() alors
alors ![]() et
et ![]() d’où le résultat.
d’où le résultat.
Montrons ensuite que pour tous ![]() tels que
tels que ![]() les nombres
les nombres ![]() et
et ![]() sont en progression géométrique.
sont en progression géométrique.
Si l’un des 3 nombres est nul, par exemple ![]() on a immédiatement :
on a immédiatement : ![]() ce qui implique
ce qui implique ![]() ou
ou ![]() Si
Si ![]() alors pour tout
alors pour tout ![]() les nombres
les nombres ![]() et
et ![]() sont en progression géométrique. Et de même si
sont en progression géométrique. Et de même si ![]()
Supposons maintenant ![]() et
et ![]() tous non nuls et posons pour tout
tous non nuls et posons pour tout ![]() :
:
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}P\left(\dfrac{b^{2}}{c}\right) & = & \left(\left(b+c\right)\dfrac{b^{2}}{c}+bc\right)^{3}-b^{3}\left(\dfrac{b^{2}}{c}+b+c\right)^{3}\\& = & \left(\dfrac{b}{c}\right)^{3}\left[\left(b^{2}+bc+c^{2}\right)^{3}-\left(b^{2}+bc+c^{2}\right)^{3}\right]\\& = & 0\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-5ac4bb65fa43ff015225728963ed113e_l3.png)
![]()
- si
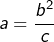 alors
alors 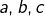 sont en progression géométrique.
sont en progression géométrique. - si
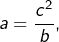 idem.
idem. - Enfin, si
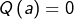 alors
alors 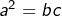 (puisque
(puisque 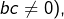 ce qui prouve encore que
ce qui prouve encore que 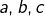 sont en progression géométrique.
sont en progression géométrique.
Solution 2
En développant chaque membre de l’égalité, on obtient d’une part :
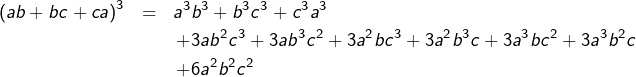
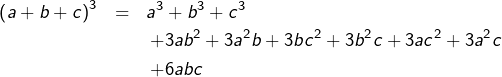
![]()
![]()
Pour consulter l’énoncé, c’est ici

