Solution pour le challenge 8
Afin de tracer avec justesse le graphe demandé, il sera utile de connaître ses intersections avec l’axe des abscisses. Résolvons donc l’équation :
![]()
Visiblement, 0 et 1 sont solutions, d’où l’existence de deux réels ![]() tels que, pour tout
tels que, pour tout ![]() :
:![]()
Par identification des coefficients :
![]()
L’équation ![]() équivaut donc à
équivaut donc à ![]() càd
càd ![]()
et ses solutions sont -2, 0 et 1.
Etudions à présent les variations de ![]() Pour tout
Pour tout ![]() :
:
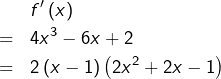
Les racines du trinôme ![]() sont :
sont :
![Rendered by QuickLaTeX.com \[\boxed{x_{1}=\frac{-1-\sqrt{3}}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9d72d40930b731bdb6a009ff41ccd723_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{x_{2}=\frac{-1+\sqrt{3}}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ac8544b15ff81c92f019fe8239c68a33_l3.png)
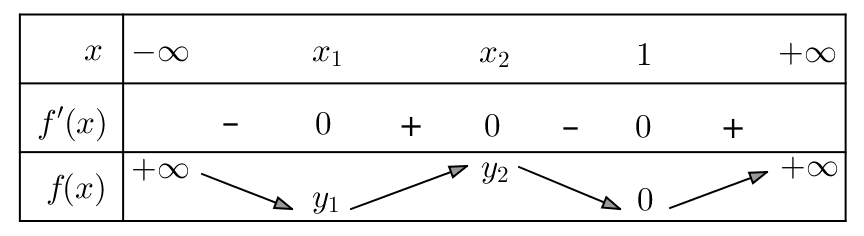
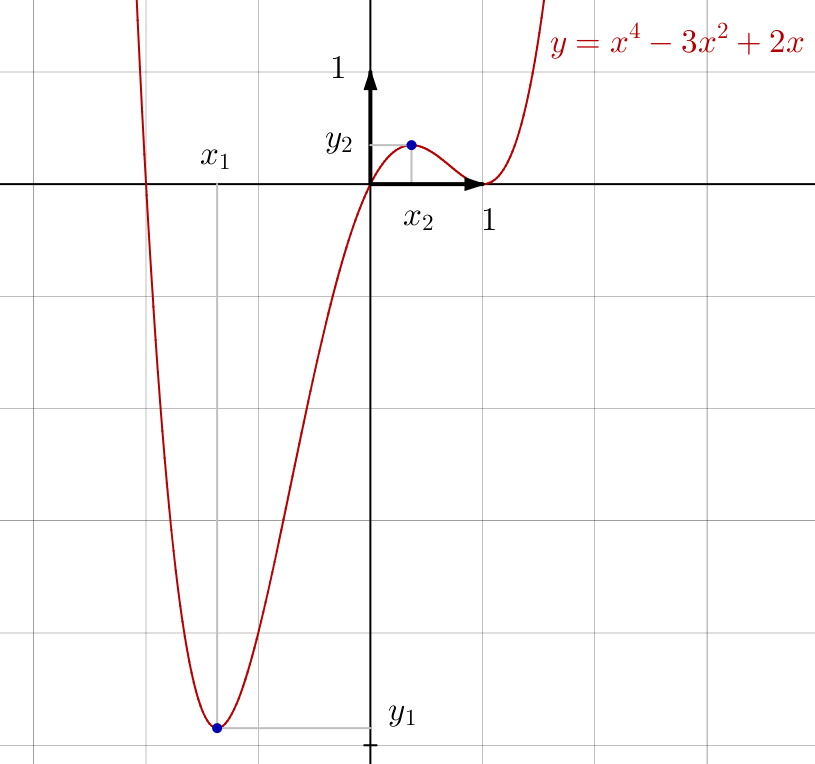
Notons encore ![]() et
et ![]() . Un petit calcul montre que :
. Un petit calcul montre que :
![Rendered by QuickLaTeX.com \[\boxed{y_{1}=\frac{-9-6\sqrt{3}}{4}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7e64c110c5c2b43cb659415c85a525ed_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{y_{2}=\frac{-9+6\sqrt{3}}{4}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-41f503eaab092fcf4a5efd675ccc294b_l3.png)
Voici le tableau des variations de ![]() :
:
et son graphe :
Passons à la preuve de l’existence d’une unique droite bitangente au graphe de ![]() c’est-à-dire tangente simultanément en deux points distincts de celui-ci.
c’est-à-dire tangente simultanément en deux points distincts de celui-ci.
On cherche deux réels ![]() tels que les tangentes à
tels que les tangentes à ![]() aux points d’abscisses
aux points d’abscisses ![]() et
et ![]() soient confondues.
soient confondues.
Pour tout ![]() :
:
![]()
![]()
L’équation de la tangente au point d’abscisse ![]() est donc :
est donc :![]()
La condition imposée prend la forme :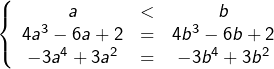
d’où :![]()
ou encore, en factorisant dans chaque égalité par ![]() et puisque
et puisque ![]() :
:
![]()
La relation ![]() fait apparaître deux cas :
fait apparaître deux cas :
- 1er cas :
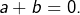 D’après (1) :
D’après (1) : 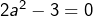 d’où
d’où 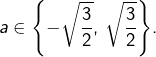
Comme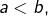 nécessairement :
nécessairement : 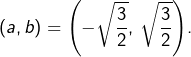
- 2ème cas :
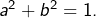 D’après (2) :
D’après (2) : 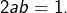 Donc, par différence
Donc, par différence 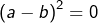 et donc
et donc 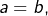 ce qui est exclu par hypothèse.
ce qui est exclu par hypothèse.
Finalement, la seule possibilité est celle obtenue au 1er cas.
Finalement :
Il existe une unique droite bitangente à ![]()
Son équation est ![]() , avec :
, avec :![]()
et![]()
soit :
![Rendered by QuickLaTeX.com \[\boxed{y=2x-\frac{9}{4}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-62ee5d0a65a863c6e27d88f1892e58b3_l3.png)
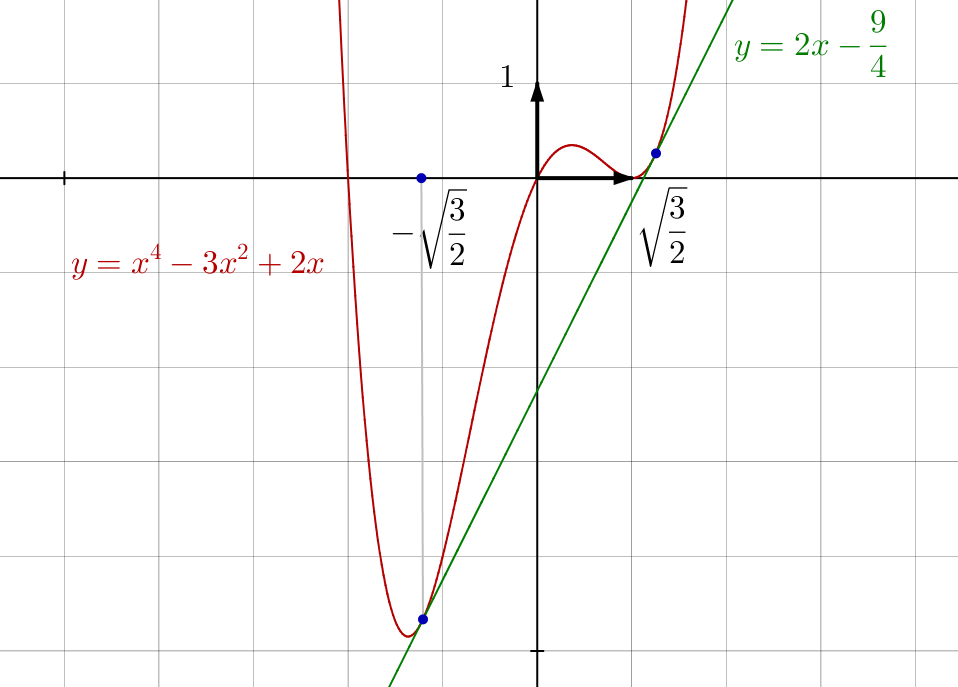
Pour finir : voici le graphe de ![]() , la droite bitangente et les deux points de contact.
, la droite bitangente et les deux points de contact.
Pour consulter l’énoncé, c’est ici

