Solution pour le challenge 76

Comme $abc>0,$ alors de deux choses l’une :

ou bien $a,b,c>0$
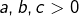
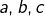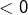ou bien deux des trois nombres $a,b,c$ sont $<0$ et le troisième est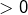 $>0$

On va prouver par l’absurde que cette seconde option est exclue.

Vue la symétrie du problème, on peut supposer par exemple :

$a\leqslant b<0<c$

Comme $c>-a-b$ alors (en multipliant par $-a-b>0)$ :

$-c\left(a+b\right)>\left(a+b\right)^{2}$

Or $ab>-c\left(a+b\right)$ et donc $ab>\left(a+b\right)^{2},$ c’est-à-dire :

$a^{2}+ab+b^{2}<0$

ou encore :

$\left(a+\frac{b}{2}\right)^{2}+\frac{3b^{2}}{4}<0$

ce qui est absurde.

Variante

Ce qui suit a été proposé par Lucas Fauvel, étudiant en MPSI. On commence comme ci-dessus, en supposant $c>0>-b\geqslant-a$ . Alors :

$c>-a-b>-a$

donc (en multipliant par $-b>0$ ) :

$-bc>ab$

et a fortiori (vu que $ca<0$ ) :

$-bc>ab+ca$

Ainsi $ab+bc+ca<0$ : c’est absurde.

A présent, on généralise …

Soit $n$ un entier supérieur ou égal à 2 et soient $a_{1},\cdots,a_{n}\in\mathbb{R}.$

Pour tout $k\in\left\llbracket 1,n\right\rrbracket$ , on note :

$e_{k}=\sum_{1\leqslant i_{1}<\cdots<i_{k}\leqslant n}a_{i_{k}}$

Les $e_{k}$ sont les expressions symétriques élémentaires en $a_{1},\cdots,a_{n}.$ Introduisons le polynôme :

$P=\prod_{i=1}^{n}\left(X+a_{i}\right)$

Son expression développée est (en posant $e_{0}=1)$ :

$P=\sum_{k=0}^{n}e_{k}X^{n-k}$

Supposons que $\forall k\in\left\llbracket 1,n\right\rrbracket ,\thinspace e_{k}>0$ et montrons par l’absurde que $\forall k\in\left\llbracket 1,n\right\rrbracket ,\thinspace a_{k}>0.$

S’il existait $j\in\left\llbracket 1,n\right\rrbracket$ tel que $a_{j}<0,$ on aurait :

$0=P\left(-a_{j}\right)=\sum_{k=0}^{n}e_{k}\left(-a_{j}\right)^{n-k}>0$

ce qui est absurde.

Une variante de cette solution nous a été communiquée par Emilien Paganelli :

On observe que, pour tout $x\geqslant0$ :

$P'\left(x\right)=\sum_{k=0}^{n-1}\left(n-k\right)e_{k}x^{n-k-1}\geqslant0$

d’où la croissance de $P$ sur $\left[0,+\infty\right[$ et donc sa stricte positivité sur cet intervalle, puisque $P\left(0\right)=e_{n}>0.$ De ce fait, les racines de $P$ sont toutes strictement négatives, ce qui donne la conclusion.

Pour consulter l’énoncé, c’est ici

Partager cet article

Variante

A présent, on généralise …

Laisser un commentaire Annuler la réponse