Solution pour le challenge 74
Notons ![]() la tangente au point d’abscisse
la tangente au point d’abscisse ![]() On commence par calculer l’abscisse
On commence par calculer l’abscisse ![]() du point d’intersection de
du point d’intersection de ![]() avec l’axe des abscisses et l’ordonnée
avec l’axe des abscisses et l’ordonnée ![]() de son point d’intersection avec l’axe des ordonnées. Pour cela, on part de l’équation de cette tangente :
de son point d’intersection avec l’axe des ordonnées. Pour cela, on part de l’équation de cette tangente :
![]()
![Rendered by QuickLaTeX.com \[\boxed{\alpha\left(a\right)=a-\frac{f\left(a\right)}{f'\left(a\right)}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e800fec9d98347ec832b3d023606743f_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\boxed{\mathcal{A}\left(a\right)=\frac{-\left(a\thinspace f'\left(a\right)-f\left(a\right)\right)^{2}}{2\thinspace f'\left(a\right)}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cbcb311df96674868605579ad4defb6f_l3.png)
Comme ![]() est décroissante et minorée par
est décroissante et minorée par ![]() elle possède en
elle possède en ![]() une limite finie
une limite finie ![]() Pour tout
Pour tout ![]() :
:
![]()
![]()
![]()
- Si
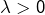 alors
alors 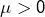 et l’expression de
et l’expression de 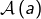 montre que :
montre que :
En effet, le numérateur tend vers![Rendered by QuickLaTeX.com \[\lim_{a\rightarrow+\infty}\mathcal{A}\left(a\right)=+\infty\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ce79005801994228a61d0fb38262df3f_l3.png)
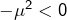 tandis que le dénominateur est négatif et tend vers
tandis que le dénominateur est négatif et tend vers 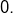
- Si
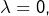 alors on peut avoir pour
alors on peut avoir pour 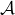 une limite finie ou infinie selon les cas. Considérons le cas de :
une limite finie ou infinie selon les cas. Considérons le cas de :
On calcule :![Rendered by QuickLaTeX.com \[ f:\left[0,+\infty\right[\rightarrow\mathbb{R},\thinspace x\mapsto\frac{1}{\left(x+1\right)^{q}}\qquad\text{avec }q>0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-72cefab07e2b0f0d22f12c6e2ec56740_l3.png)
ce qui montre déjà que![Rendered by QuickLaTeX.com \[f'\left(x\right)=-\frac{q}{\left(x+1\right)^{q+1}}<0,\qquad f''\left(x\right)=\frac{q\left(q+1\right)}{\left(x+1\right)^{q+2}}>0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c26e4a8239ce13a0ecebbabc148f512e_l3.png)
 vérifie (quel que soit
vérifie (quel que soit 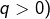 les hypothèses de l’énoncé. Ensuite :
les hypothèses de l’énoncé. Ensuite :
En choisissant![Rendered by QuickLaTeX.com \[\mathcal{A}\left(a\right)=\frac{\left(a+1\right)^{q+1}}{2q}\left(\frac{qa}{\left(a+1\right)^{q+1}}+\frac{1}{\left(a+1\right)^{q}}\right)^{2}\sim\frac{\left(q+1\right)^{2}}{2q\thinspace a^{q-1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-02fa429b665998f7fcae3e9c87b1bf1d_l3.png)
![Rendered by QuickLaTeX.com q\in\left]0,1\right[,](https://math-os.com/wp-content/ql-cache/quicklatex.com-bdbd9534edab68f9192dfef3f5713477_l3.png) la limite est
la limite est 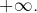 En choisissant
En choisissant 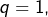 elle vaut
elle vaut 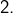 Et en choisissant
Et en choisissant 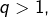 elle est nulle.
elle est nulle.
Pour consulter l’énoncé, c’est ici

