Solution pour le challenge 71
On calcule, pour tout entier ![]() :
:
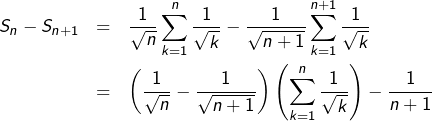
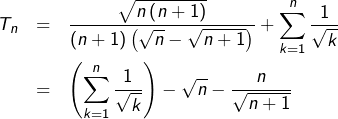
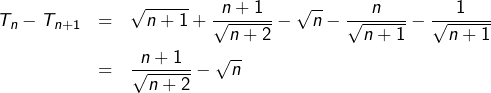
![]()
pour
Et comme ![]() alors
alors ![]() pour tout
pour tout ![]() Finalement, la suite
Finalement, la suite ![]() est croissante.
est croissante.
Remarque
Il est facile de voir que :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k=1}^{n}\frac{1}{\sqrt{k}}\sim2\sqrt{n}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cbdc0a65faf2d3c2508fde27f6afeb87_l3.png)
Pour consulter l’énoncé, c’est ici
Solution pour le challenge 71
On calcule, pour tout entier ![]() :
:
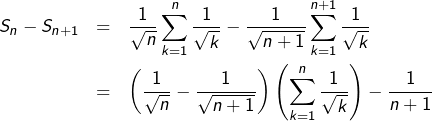
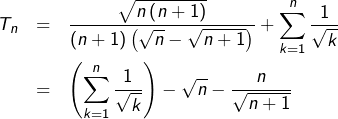
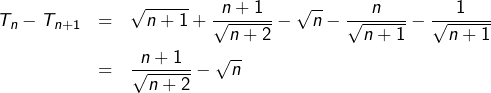
![]()
Et comme ![]() alors
alors ![]() pour tout
pour tout ![]() Finalement, la suite
Finalement, la suite ![]() est croissante.
est croissante.
Il est facile de voir que :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k=1}^{n}\frac{1}{\sqrt{k}}\sim2\sqrt{n}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cbdc0a65faf2d3c2508fde27f6afeb87_l3.png)
Pour consulter l’énoncé, c’est ici