Solution pour le challenge 70
➣ Un contre-exemple hyper classique pour commencer, la suite de terme général :
![]()
![Rendered by QuickLaTeX.com \[X_{n}=\frac{1}{n}\sum_{k=1}^{n}\left(-1\right)^{k}=\frac{\left(-1\right)^{n}-1}{2n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c8bc8466e330204c0bf8f80019edb809_l3.png)
![]()
➣ Ensuite, si l’on veut une suite ![]() divergente pour laquelle la suite
divergente pour laquelle la suite ![]() diverge, on peut proposer :
diverge, on peut proposer :
![]()
![Rendered by QuickLaTeX.com \[X_{n}=\frac{1}{n}\sum_{k=1}^{n}\left(-1\right)^{k}k\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-72f75a80c1942cb02c5817fb7919704e_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}\left(-1\right)^{k}k=\left(-1\right)^{n}\left\lfloor \frac{n+1}{2}\right\rfloor\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-496d366f220db6f385bc1abf4952c3fd_l3.png)
![]()
![]()
➣ Dans l’exemple précédent, la suite ![]() n’était pas bornée. Voici maintenant un exemple d’une suite
n’était pas bornée. Voici maintenant un exemple d’une suite ![]() bornée et divergente, pour laquelle la suite
bornée et divergente, pour laquelle la suite ![]() diverge. Notons
diverge. Notons ![]() le logarithme binaire (alias : logarithme en base 2) et posons, pour tout
le logarithme binaire (alias : logarithme en base 2) et posons, pour tout ![]() :
:
![]()
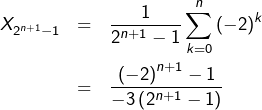
![Rendered by QuickLaTeX.com \[\boxed{X_{2^{n+1}-1}=-\frac{1}{3}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3b37d8df7203f765371ef70c1e259f10_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*}X_{2^{n+1}-2} & = & \frac{1}{2^{n+1}-2}\left[\left(\sum_{k=0}^{n}\left(-2\right)^{k}\right)-\left(-1\right)^{n}\right]\\& = & \frac{\left(-2\right)^{n+1}-1}{-3\left(2^{n+1}-2\right)}-\frac{\left(-1\right)^{n}}{2^{n+1}-2}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-2b6e6e9746e6744281c21f28ae37c29b_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{X_{2^{n+1}-2}=\frac{1}{3}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-568d75c321db245d458b4cb021db1d46_l3.png)
Pour consulter l’énoncé, c’est ici


OK, logique en fin de compte. J’ai bien cherché comment alterner des suites de 1 et de -1, mais je ne sais pas pourquoi je n’ai pas pensé au puissances de 2 pour les longueurs, maintenant ça me parait tellement évident ! J’avais essayé les carrés, les cubes, et j’avais vu plus généralement qu’avec des suites de 1 et de -1 alternées de longueur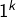 ,
, 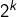 ,
, 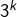 , etc ça ne pouvait pas marcher. Après j’étais parti dans d’autres délires comme des sommes trigonométriques, je n’ai pas trop insisté, mais je vois que j’ai quand même manqué de lucidité sur ce coup !
, etc ça ne pouvait pas marcher. Après j’étais parti dans d’autres délires comme des sommes trigonométriques, je n’ai pas trop insisté, mais je vois que j’ai quand même manqué de lucidité sur ce coup !