Solution pour le challenge 66
Il est connu que, pour tout ![Rendered by QuickLaTeX.com x\in\left]-1,1\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d3a1d8c80a298f2939e44e3a38c70a88_l3.png) :
:
![Rendered by QuickLaTeX.com \[\boxed{\ln\left(1+x\right)=\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n-1}}{n}\thinspace x^{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c336e699605dfa70ed9e12210d21935d_l3.png)
Si cette formule ne vous est pas familière, une preuve élémentaire en est donnée
plus bas.
En prenant 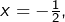 on trouve :
on trouve :
![Rendered by QuickLaTeX.com \[\ln\left(\frac{1}{2}\right)=\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n-1}}{n}\thinspace\left(-\frac{1}{2}\right)^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d7733591e354fa34ff7b9367c573e435_l3.png)
soit, après simplification :
![Rendered by QuickLaTeX.com \[\boxed{\ln\left(2\right)=\sum_{n=1}^{\infty}\frac{1}{n\thinspace2^{n}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6d96fe680b8a5dc2719f32db7a0035fd_l3.png)
On peut exploiter ce développement en série pour obtenir des majorations non triviales de
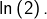
En effet, pour tout entier
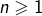
:
![Rendered by QuickLaTeX.com \[\ln\left(2\right)=L_{n}+R_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8656cf0f47ef1aa3488f83995a965a48_l3.png)
où l’on a posé :
![Rendered by QuickLaTeX.com \[L_{n}=\sum_{k=1}^{n}\frac{1}{k\thinspace2^{k}}\qquad\text{et}\qquad R_{n}=\sum_{k=n+1}^{\infty}\frac{1}{k\thinspace2^{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fa1e6e2550b32ac5db58a779ab29b02f_l3.png)
En outre :
![Rendered by QuickLaTeX.com \[R_{n}<\frac{1}{n+1}\thinspace\sum_{k=n+1}^{\infty}\frac{1}{2^{k}}=\frac{1}{2^{n}\left(n+1\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-653ea388134190a0a4ef5fd50be3413c_l3.png)
et par conséquent :
![Rendered by QuickLaTeX.com \[\boxed{\forall n\in\mathbb{N}^{\star},\thinspace\ln\left(2\right)<L_{n}+\frac{1}{2^{n}\left(n+1\right)}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-12e3d06064bdfe2132c3466d370dddc8_l3.png)
➣ Pour 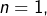 cette majoration donne
cette majoration donne 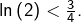
➣ Pour 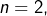 on obtient :
on obtient : 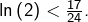
➣ Pour 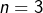 :
: 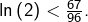 Or
Or 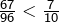 puisque
puisque 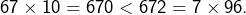 Nous avons donc bien prouvé que :
Nous avons donc bien prouvé que :
![Rendered by QuickLaTeX.com \[\boxed{\ln\left(2\right)<\frac{7}{10}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ed257ddf9416ff62a6f7770af9ea60e2_l3.png)
Ajoutons qu’avec ce qui précède, on peut aussi minorer 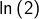 par
par 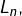 quel que soit
quel que soit  Par exemple, pour
Par exemple, pour 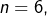 il vient :
il vient :
![Rendered by QuickLaTeX.com \[\ln\left(2\right)>\frac{1}{2}+\frac{1}{8}+\frac{1}{24}+\frac{1}{64}+\frac{1}{160}+\frac{1}{384}>\frac{69}{100}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-052d5f0e69a0ed5c77763d6d0b6256d4_l3.png)
On pourra retenir l’encadrement à
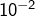
près suivant :
![Rendered by QuickLaTeX.com \[\boxed{0.69<\ln\left(2\right)<0.70}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-809363d476975cd484575137dbfa3cfc_l3.png)
Remarque
Dans la formule
![Rendered by QuickLaTeX.com \[\ln\left(1+x\right)=\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n-1}}{n}\thinspace x^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-36de347fed484c89a00cbf770c45efe5_l3.png)
qui est valable pour tout
![Rendered by QuickLaTeX.com x\in\left]-1,1\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d3a1d8c80a298f2939e44e3a38c70a88_l3.png)
, on aurait pu tout simplement choisir
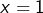
pour obtenir :
![Rendered by QuickLaTeX.com \[\ln(2)=\sum_{n=1}^\infty\frac{(-1)^{n-1}}{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3318209dcca3359b89628b1a69f5812b_l3.png)
puis en déduire une valeur approchée de
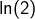
en considérant une somme partielle suffisamment « longue ». Le problème est que cette série alternée converge trop lentement pour produire une approximation acceptable à peu de frais. Qu’on en juge (calculs réalisés avec Maple) :
![Rendered by QuickLaTeX.com \[\ln(2)\simeq0,6931471805599453094172321\text{ à }10^{-25}\text{ près}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-aa6ab9b07df649c1583940e54a86dad6_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{100}\frac{1}{k\,2^k}\simeq0,6931471805599453094172321\text{ à }10^{-25}\text{ près}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-11095f2c8d68d980d4e945f0f786f5b5_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{100}\frac{(-1)^{k-1}}{k}\simeq0,6881721793101952032446459\text{ à }10^{-25}\text{ près}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bfdf8d32acd11c4cdccaf9ff23e4ca9e_l3.png)
Avec 100 termes, la série alternée fournit un résultat médiocre (écart de l’ordre de
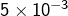
) alors que l’autre série donne une approximation excellente (on peut vérifier que l’écart est inférieur à
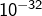
).
Proposition
Pour tout ![Rendered by QuickLaTeX.com x\in\left]-1,1\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d3a1d8c80a298f2939e44e3a38c70a88_l3.png) :
:
![Rendered by QuickLaTeX.com \[\ln\left(1+x\right)=\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n-1}}{n}\thinspace x^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-36de347fed484c89a00cbf770c45efe5_l3.png)
Preuve (cliquer pour déplier / replier)
On part de la formule explicite pour une somme géométrique.
Pour tout  et tout
et tout 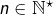 :
:
![Rendered by QuickLaTeX.com \[\sum_{k=0}^{n-1}\left(-1\right)^{k}t^{k}=\frac{1-\left(-1\right)^{n}t^{n}}{1+t}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8f54745ca792157195891e12deeb0728_l3.png)
Ensuite, on intègre sur entre 0 et
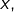
pour
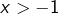
:
![Rendered by QuickLaTeX.com \[\sum_{k=0}^{n-1}\left(-1\right)^{k}\int_{0}^{x}t^{k}\thinspace dt=\int_{0}^{x}\frac{1}{1+t}\thinspace dt-\left(-1\right)^{n}\int_{0}^{x}\frac{t^{n}}{1+t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e19be341a0ab74f5218613fdcc52f987_l3.png)
Autrement dit :
![Rendered by QuickLaTeX.com \[\ln\left(1+x\right)=\sum_{k=0}^{n-1}\frac{\left(-1\right)^{k}}{k+1}\thinspace x^{k+1}+\left(-1^{n}\right)\int_{0}^{x}\frac{t^{n}}{1+t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a2b53330e7fec500b4eb27b7e474db1e_l3.png)
Il reste à prouver que, si
![Rendered by QuickLaTeX.com x\in\left]-1,1\right],](https://math-os.com/wp-content/ql-cache/quicklatex.com-2fa856155525e9e3c23febb5fe56c84e_l3.png)
alors cette dernière intégrale tend vers 0 lorsque

tend vers
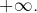
Notons donc :
![Rendered by QuickLaTeX.com \[R_{n}\left(x\right)=\int_{0}^{x}\frac{t^{n}}{1+t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fc5e69cd7450d61f8e7f68ff61c27a2c_l3.png)
et distinguons deux cas selon que
![Rendered by QuickLaTeX.com x\in\left[0,1\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-07b514b1e0c7996db17eecb846a1a881_l3.png)
ou que
![Rendered by QuickLaTeX.com x\in\left]-1,0\right[.](https://math-os.com/wp-content/ql-cache/quicklatex.com-13a6a9afcf4bcf6ffe96d3d2b776bd85_l3.png)
➣ 1er cas – On suppose ![Rendered by QuickLaTeX.com x\in\left[0,1\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-07b514b1e0c7996db17eecb846a1a881_l3.png) , alors :
, alors :
![Rendered by QuickLaTeX.com \[0\leqslant R_{n}\left(x\right)\leqslant\int_{0}^{x}t^{n}\thinspace dt=\frac{x^{n+1}}{n+1}\leqslant\frac{1}{n+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-936fc780d000eb51b2f04274a1340628_l3.png)
et donc
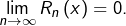
➣ 2ème cas – On suppose ![Rendered by QuickLaTeX.com x\in\left]-1,0\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-30c5ac128a25e8c1d8a32a7bfb04e0b9_l3.png) et l’on effectue le changement de variable
et l’on effectue le changement de variable 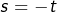 :
:
![Rendered by QuickLaTeX.com \[R_{n}\left(x\right)=-\int_{x}^{0}\frac{t^{n}}{1+t}\thinspace dt=\left(-1\right)^{n+1}\int_{0}^{-x}\frac{s^{n}}{1-s}\thinspace ds\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-42e0607a76aae0ab9b7a218599ffb6f4_l3.png)
donc :
![Rendered by QuickLaTeX.com \[\left|R_{n}\left(x\right)\right|=\int_{0}^{-x}\frac{s^{n}}{1-s}\thinspace ds\leqslant\frac{1}{1+x}\int_{0}^{-x}\thinspace s^{n}\thinspace ds=\frac{\left(-x\right)^{n+1}}{\left(n+1\right)\left(1+x\right)}\leqslant\frac{1}{\left(n+1\right)\left(1+x\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-30dceae451f3cbaac1a79492ba5cc030_l3.png)
d’où, à nouveau,
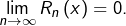
Pour consulter l’énoncé, c’est ici
![]() :
:![Rendered by QuickLaTeX.com \[\boxed{\ln\left(1+x\right)=\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n-1}}{n}\thinspace x^{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c336e699605dfa70ed9e12210d21935d_l3.png)
![]() on trouve :
on trouve :![Rendered by QuickLaTeX.com \[\ln\left(\frac{1}{2}\right)=\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n-1}}{n}\thinspace\left(-\frac{1}{2}\right)^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d7733591e354fa34ff7b9367c573e435_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\ln\left(2\right)=\sum_{n=1}^{\infty}\frac{1}{n\thinspace2^{n}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6d96fe680b8a5dc2719f32db7a0035fd_l3.png)
![]()
![Rendered by QuickLaTeX.com \[L_{n}=\sum_{k=1}^{n}\frac{1}{k\thinspace2^{k}}\qquad\text{et}\qquad R_{n}=\sum_{k=n+1}^{\infty}\frac{1}{k\thinspace2^{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fa1e6e2550b32ac5db58a779ab29b02f_l3.png)
![Rendered by QuickLaTeX.com \[R_{n}<\frac{1}{n+1}\thinspace\sum_{k=n+1}^{\infty}\frac{1}{2^{k}}=\frac{1}{2^{n}\left(n+1\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-653ea388134190a0a4ef5fd50be3413c_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\forall n\in\mathbb{N}^{\star},\thinspace\ln\left(2\right)<L_{n}+\frac{1}{2^{n}\left(n+1\right)}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-12e3d06064bdfe2132c3466d370dddc8_l3.png)
![]() cette majoration donne
cette majoration donne ![]()
![]() on obtient :
on obtient : ![]()
![]() :
: ![]() Or
Or ![]() puisque
puisque ![]() Nous avons donc bien prouvé que :
Nous avons donc bien prouvé que :![Rendered by QuickLaTeX.com \[\boxed{\ln\left(2\right)<\frac{7}{10}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ed257ddf9416ff62a6f7770af9ea60e2_l3.png)
![]() par
par ![]() quel que soit
quel que soit ![]() Par exemple, pour
Par exemple, pour ![]() il vient :
il vient :![]()
![]()
![Rendered by QuickLaTeX.com \[\ln\left(1+x\right)=\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n-1}}{n}\thinspace x^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-36de347fed484c89a00cbf770c45efe5_l3.png)
![Rendered by QuickLaTeX.com \[\ln(2)=\sum_{n=1}^\infty\frac{(-1)^{n-1}}{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3318209dcca3359b89628b1a69f5812b_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{100}\frac{1}{k\,2^k}\simeq0,6931471805599453094172321\text{ à }10^{-25}\text{ près}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-11095f2c8d68d980d4e945f0f786f5b5_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{100}\frac{(-1)^{k-1}}{k}\simeq0,6881721793101952032446459\text{ à }10^{-25}\text{ près}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bfdf8d32acd11c4cdccaf9ff23e4ca9e_l3.png)
![]() :
:![Rendered by QuickLaTeX.com \[\ln\left(1+x\right)=\sum_{n=1}^{\infty}\frac{\left(-1\right)^{n-1}}{n}\thinspace x^{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-36de347fed484c89a00cbf770c45efe5_l3.png)
![]() et tout
et tout ![]() :
:![Rendered by QuickLaTeX.com \[\sum_{k=0}^{n-1}\left(-1\right)^{k}t^{k}=\frac{1-\left(-1\right)^{n}t^{n}}{1+t}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8f54745ca792157195891e12deeb0728_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=0}^{n-1}\left(-1\right)^{k}\int_{0}^{x}t^{k}\thinspace dt=\int_{0}^{x}\frac{1}{1+t}\thinspace dt-\left(-1\right)^{n}\int_{0}^{x}\frac{t^{n}}{1+t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e19be341a0ab74f5218613fdcc52f987_l3.png)
![Rendered by QuickLaTeX.com \[\ln\left(1+x\right)=\sum_{k=0}^{n-1}\frac{\left(-1\right)^{k}}{k+1}\thinspace x^{k+1}+\left(-1^{n}\right)\int_{0}^{x}\frac{t^{n}}{1+t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a2b53330e7fec500b4eb27b7e474db1e_l3.png)
![]()
![]() , alors :
, alors :![]()
![]() et l’on effectue le changement de variable
et l’on effectue le changement de variable ![]() :
:![]()
![]()

