Solution pour le challenge 61
Clairement, ![]() convient.
convient.
Supposons maintenant que ![]() et qu’il existe
et qu’il existe ![]() tel que
tel que ![]()
Alors ![]() donc
donc ![]() et
et ![]() sont des diviseurs de
sont des diviseurs de ![]() d’où l’existence de
d’où l’existence de ![]() tels que :
tels que :
![]()
Mais alors :
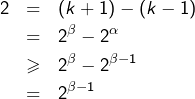
Si ![]() alors
alors ![]() d’où
d’où ![]() : c’est impossible. Donc
: c’est impossible. Donc ![]() ce qui entraîne
ce qui entraîne ![]() puis
puis ![]()
Réciproquement, ![]() convient puisque
convient puisque ![]()
Remarque
L’entier 3 est donc le seul entier ![]() tel que
tel que ![]() soit un carré parfait, quel que soit
soit un carré parfait, quel que soit ![]()
En effet :
- 3 convient puisque :
![Rendered by QuickLaTeX.com \displaystyle{1^{3}+2^{3}+\cdots+n^{3}=\left[\frac{n\left(n+1\right)}{2}\right]^{2}}](https://math-os.com/wp-content/ql-cache/quicklatex.com-b7309328eac393e11021693c8819705b_l3.png) pour tout
pour tout 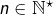 .
. - si
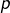 convient, alors en particulier
convient, alors en particulier 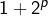 est un carré parfait et ce qui précède s’applique.
est un carré parfait et ce qui précède s’applique.
Pour consulter l’énoncé, c’est ici

