Solution pour le challenge n° 6

Solution pour le challenge 6

La série proposée converge, par comparaison avec une série géométrique; en effet si l’on pose $q=1-2^{-n},$ alors pour tout $k\in\mathbb{N}$ :

$2^{k}\geqslant k$

et donc :

$0\leqslant q^{2^{k}}\leqslant q^{k}$

Afin d’établir l’inégalité demandée, on va « couper la série en deux » et montrer …

d’une part, que :
$\sum_{k=0}^{n-1}\left(1-2^{-n}\right)^{2^{k}}<n\qquad\left(\spadesuit\right)$
et d’autre part, que :
$\sum_{k=n}^{\infty}\left(1-2^{-n}\right)^{2^{k}}<1\qquad\left(\clubsuit\right)$

Il suffira, pour conclure, d’ajouter membre à membre ces deux inégalités.

L’inégalité $\left(\spadesuit\right)$ est évidente : la somme comporte $n$ termes et chacun est majoré (strictement) par $1.$

Il reste donc à prouver $\left(\clubsuit\right).$

On sait (inégalité de Bernoulli) que, si $\epsilon>0$ et si $p$ est un entier supérieur ou égal à 2, alors :

$\left(1+\epsilon\right)^{p}>1+p\epsilon$

En choisissant $\epsilon=\frac{1}{p}$ :

$\left(1+\frac{1}{p}\right)^{p}>2$

ou encore :

$\left(1-\frac{1}{p+1}\right)^{p}<\frac{1}{2}$

En choisissant maintenant $p=2^{n}-1$ :

$\left(1-2^{-n}\right)^{2^{n}-1}<\frac{1}{2}$

A fortiori :

$\left(1-2^{-n}\right)^{2^{n}}<\frac{1}{2}$

On voit alors que :

$\begin{eqnarray*}& &\sum_{k=n}^{\infty}\left(1-2^{-n}\right)^{2^{k}}\\& = & \sum_{k=n}^{\infty}\left[\left(1-2^{-n}\right)^{2^{n}}\right]^{2^{k-n}}\\& = & \sum_{k=0}^{\infty}\left[\left(1-2^{-n}\right)^{2^{n}}\right]^{2^{k}}\end{eqnarray*}$

et donc :

$\begin{eqnarray*}& &\sum_{k=n}^{\infty}\left(1-2^{-n}\right)^{2^{k}}\\& < & \sum_{k=0}^{\infty}\left(\frac{1}{2}\right)^{2^{k}}\\& < & \sum_{k=1}^{\infty}\left(\frac{1}{2}\right)^{k}=1\end{eqnarray*}$

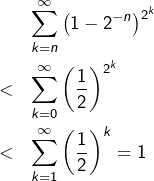
Pour consulter l’énoncé, c’est ici

Partager cet article

Laisser un commentaire Annuler la réponse