Solution pour le challenge 5
Etape 1
Soit ![]()
En remplaçant ![]() par 0 dans
par 0 dans ![]() :
:
![]()
Ceci montre que si ![]() alors :
alors :
![]()
On suppose désormais que ![]()
Etape 2
Soient ![]() quelconque et
quelconque et ![]() En appliquant
En appliquant ![]() …
…
➣ au couple ![]() , on trouve :
, on trouve :
![]()
➣ au couple ![]() , on trouve :
, on trouve :
![]()
Il en résulte que :
![]()
En particulier, pour ![]() :
:
![]()
![]()
Ceci montre que ![]()
Etape 3
Si ![]() on obtient en appliquant
on obtient en appliquant ![]() pour le couple
pour le couple ![]() :
:
![]()
Donc :
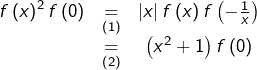
puis, en simplifiant par ![]() (dont on rappelle qu’il est non nul…) :
(dont on rappelle qu’il est non nul…) :
![]()
Etape 4
En appliquant ![]() au couple
au couple ![]() pour
pour ![]() :
:
![]()
![]()
![]()
En confrontant ![]() et
et ![]() on conclut que, pour tout réel non nul
on conclut que, pour tout réel non nul ![]() :
:
![]()
Cette égalité vaut encore pour ![]() En effet, en appliquant
En effet, en appliquant ![]() au couple
au couple ![]() on trouve
on trouve ![]() et comme
et comme ![]() (on sait maintenant que
(on sait maintenant que ![]() alors
alors ![]()
Etape 5 : conclusion
Deux solutions possibles pour l’équation fonctionnelle proposée :
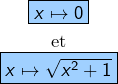
Chacune d’elles convient effectivement.
Pour consulter l’énoncé, c’est ici

