Solution pour le challenge 46
Nous allons prouver que :
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}\mu_{n}=\frac{1}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f67e34997bdfa90ef1d18fede107fdb1_l3.png)
Une solution rapide consiste à établir au préalable les deux points suivants :
Lemme 1 – Pour tout entier ![]() et pour
et pour ![]() :
:
![]()
Lemme 2 – Il existe une suite
![]()
Le lemme 1 (combiné avec le fait que ![]() est continue et admet
est continue et admet ![]() pour limite en
pour limite en ![]() comme en
comme en ![]() garantit l’existence d’un minimum absolu
garantit l’existence d’un minimum absolu ![]() tel que
tel que ![]()
Ensuite, l’encadrement :
![]()
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}\mu_{n}=\frac{1}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f67e34997bdfa90ef1d18fede107fdb1_l3.png)
Passons aux preuves des deux lemmes.
Preuve du lemme 1
Soit ![]() Distinguons trois cas, selon la valeur de
Distinguons trois cas, selon la valeur de ![]()
Cas 1 : ![]()
On observe que :
![Rendered by QuickLaTeX.com \[P_{n}\left(x\right)=1+\sum_{k=1}^{n}x^{2k-1}\left(1+x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a323ecfc5e02c61d078a104b873bcf35_l3.png)
Cas 2 : ![]()
On utilise la formule habituelle pour les sommes géométriques.
Vue l’imparité de l’exposant ![]() :
:
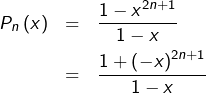
![]()
Cas 3 : ![]()
On minore la somme qui définit ![]() par son premier terme, ce qui donne
par son premier terme, ce qui donne ![]()
Lemme 2
Posons :
![]()
On sait que ![]()
Donc, en observant que pour tout ![]() :
:
![]()
![]()
Ainsi :
![]()
Variations de 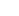
Pour tout ![]() et tout
et tout ![]() :
:
![]()
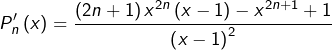
Notons désormais ![]() le numérateur de cette dernière fraction. Alors :
le numérateur de cette dernière fraction. Alors :![]() donc :
donc :![]()
![]()
Ceci montre que ![]() est du même signe de
est du même signe de ![]() Par conséquent :
Par conséquent :
➡ ![]() est strictement croissante sur
est strictement croissante sur ![]() et sur
et sur ![]()
➡ ![]() est strictement décroissante sur l’intervalle
est strictement décroissante sur l’intervalle ![]()
Comme de plus :
![]()
![]()
En outre ![]() et les variations de
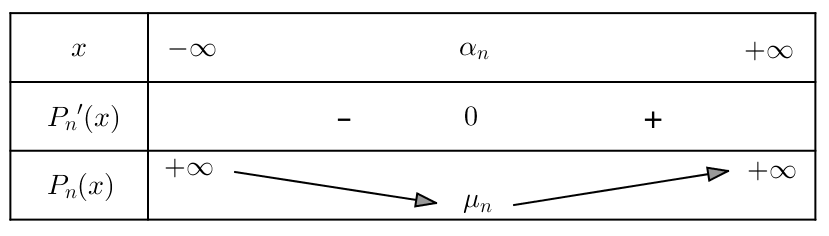
et les variations de ![]() sont récapitulées ci-dessous :
sont récapitulées ci-dessous :
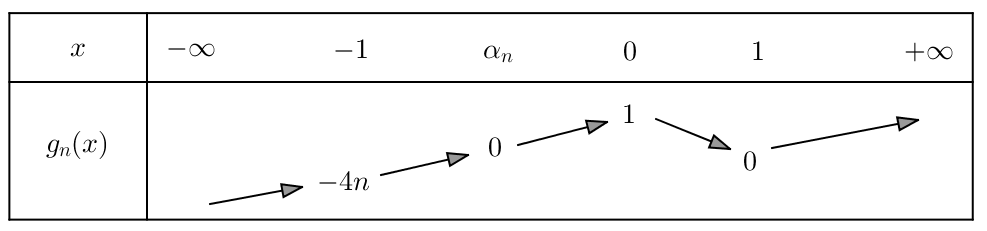
On connaît ainsi le signe de ![]() (c’est-à-dire celui de
(c’est-à-dire celui de ![]() et donc les variations de
et donc les variations de ![]() En particulier, ceci confirme de l’existence d’un minimum absolu pour
En particulier, ceci confirme de l’existence d’un minimum absolu pour ![]() :
:
![]()
Pour consulter l’énoncé, c’est ici

