Solution pour le challenge 45
Ce challenge est lié à un aspect élémentaire de la théorie des groupes.
Les opérations T et H peuvent, en effet, être vues comme des éléments du groupe symétrique ![]() et tout revient à expliquer qu’elles engendrent, à elles seules, le groupe entier.
et tout revient à expliquer qu’elles engendrent, à elles seules, le groupe entier.
En partant d’une permutation quelconque abcdefgh des chiffres 1 à 8 et en effectuant (dans cet ordre) :
H H T H H T H H T H
on obtient bacdefgh. On a simplement échangé les deux premiers chiffres, comme le montre la petite vidéo ci-dessous :
Notons ![]() cette permutation :
cette permutation : ![]() (c’est une transposition).
(c’est une transposition).
En partant toujours de abcdefgh et en appliquant H sept fois de suite, on obtient bcdefgha, ce qui revient à appliquer la permutation inverse de ![]() (et c’est logique vu que :
(et c’est logique vu que : ![]() ).
).
Notons C cette permutation : ![]() (c’est un cycle de longueur 8).
(c’est un cycle de longueur 8).
Voici maintenant l’argument-clef : ![]() est une partie génératrice du groupe
est une partie génératrice du groupe ![]() (ce point est un cas particulier d’un résultat détaillé en annexe). Autrement dit, toutes les permutations (il y en a au total
(ce point est un cas particulier d’un résultat détaillé en annexe). Autrement dit, toutes les permutations (il y en a au total ![]() s’obtiennent en composant entre elles
s’obtiennent en composant entre elles ![]() et
et ![]() et donc, in fine, en composant entre elles
et donc, in fine, en composant entre elles ![]() et
et ![]() ce qui règle la question.
ce qui règle la question.
Annexe – une partie génératrice de 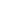
Etant donné un entier ![]() notons
notons ![]() et
et ![]() deux éléments particuliers du groupe
deux éléments particuliers du groupe ![]() :
:
➡ ![]() désigne la transposition
désigne la transposition ![]() : les entiers 1 et 2 sont échangés; tous les autres sont fixes.
: les entiers 1 et 2 sont échangés; tous les autres sont fixes.
➡ ![]() désigne le cycle
désigne le cycle ![]() :
:
- pour tout
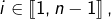 l’image de
l’image de 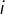 est
est 
- l’image de
 est 1
est 1
Notons ![]() le sous-groupe de
le sous-groupe de ![]() engendré par
engendré par ![]() et prouvons deux lemmes :
et prouvons deux lemmes :
[Lemme 1] pour tout ![]() , la transposition
, la transposition ![]() appartient à
appartient à ![]()
[Lemme 2] toute transposition est produit de transpositions du type ![]()
Il en résultera que ![]() contient toutes les transpositions.
contient toutes les transpositions.
Or, il est classique que celles-ci engendrent ![]() d’où la conclusion :
d’où la conclusion :
![]()
Le cas particulier n = 8 permet de traiter le challenge.
Voici le détail pour chacun des deux lemmes :
Preuve du lemme 1
Montrons que, pour tout ![]() :
:![]()
➡ l’égalité est évidente pour ![]()
➡ En la supposant vraie pour un certain ![]() :
:
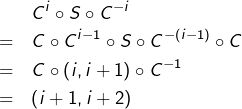
Preuve du lemme 2
Pour tout ![]() , notons
, notons ![]() la transposition
la transposition ![]() , qui échange
, qui échange ![]() et
et ![]() .
.
Etant donnés ![]() tels que
tels que ![]() , on constate que :
, on constate que :![]()
Par exemple (dans ![]() pour
pour ![]() ) :
) :![]()
Une solution voisine de celle publiée ci-dessus a été obtenue par Alexandre Boyer, étudiant en section MP* au lycée Thiers (Marseille).
Pour consulter l’énoncé, c’est ici

