icone-challenge-math-OS

Solution pour le challenge 34

Il suffit de prouver l’existence d’une injection E\rightarrow F et d’une injection F\rightarrow E puis d’invoquer le théorème de Cantor-Bernstein.

INJECTION E\rightarrow F

On sait que l’ensemble \mathbb{Q} des nombres rationnels est dénombrable (voir par exemple ici). Autrement dit, il existe une bijection r:\mathbb{N}\rightarrow\mathbb{Q}.

Considérons l’application :

    \[$E\rightarrow F,\thinspace\varphi\mapsto\varphi\circ r\]

Cette application est injective, car si \varphi,\psi:\mathbb{R}\rightarrow\mathbb{R} sont continues et telles que \varphi\circ r=\psi\circ r, alors \varphi=\psi car \mathbb{Q} est une partie dense de \mathbb{R} et deux applications continues qui coïncident sur une telle partie sont égales (pour le détail de cette affirmation, déplier le paragraphe ci-dessous).

Détail

Notons D une partie dense de \mathbb{R}. Rappelons que cette affirmation signifie que tout nombre réel est la limite d’une suite à termes dans D.

Soient maintenant deux applications f,g:\mathbb{R}\rightarrow\mathbb{R} continues et telles que :

    \[\forall d\in D,\thinspace f\left(d\right)=g\left(d\right)\]

Etant donné x\in\mathbb{R}, il existe par hypothèse une suite \left(d_{n}\right)_{n\in\mathbb{N}} à termes dans D telle que :

    \[\lim_{n\rightarrow\infty}d_{n}=x\]

Comme f et g sont continues en x, on constate que :

    \[f\left(x\right)=\lim_{n\rightarrow\infty}f\left(d_{n}\right)=\lim_{n\rightarrow\infty}g\left(d_{n}\right)=g\left(x\right)\]

INJECTION F\rightarrow E

Etant donnée une quelconque suite u de nombres réels, notons f_{u} l’application de \mathbb{R} dans \mathbb{R} définie de la manière suivante :

  • \forall t\in\left]-\infty,0\right],\thinspace f_{u}\left(t\right)=u_{0}
  • \forall n\in\mathbb{N}^{\star},\thinspace f_{u}\left(n\right)=u_{n}
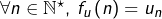
  • pour tout 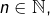n\in\mathbb{N}, la restriction de 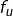f_{u} à tout segment \left[n,n+1\right] est affine

L’animation ci-dessous permet de visualiser cette définition. Le graphe de la restriction de f_{u} à l’intervalle \left[-3,9\right] est dessiné en plusieurs étapes …

Illustration Dynamique

rgbExplorer

L’application F\rightarrow E qui à toute suite u fait correspondre f_{u} est clairement injective.

En effet si u,v sont deux suites réelles telles que f_{u}=f_{v}, alors en particulier f_{u}\left(n\right)=f_{v}\left(n\right) pour tout n\in\mathbb{N}; autrement dit u=v.

Pour consulter l’énoncé, c’est ici

Partager cet article
    

Laisser un commentaire