Solution pour le challenge n° 32

Solution pour le challenge 32

Pour toute partie $B$ de $E,$ notons $1_{B}$ sa fonction indicatrice.

Rappelons que, par définition :
$\displaystyle{ 1_{B}:E\rightarrow\left\{0,1\right\} ,\thinspace x\mapsto\left\{\begin{array}{cc} 1 & \text{si }x\in B\\ 0 & \text{sinon} \end{array}\right.}$

L’hypothèse dit que l’application :
$\varphi:E\rightarrow\left\{0,1\right\} ^{m},\thinspace x\mapsto\left(1_{A_{1}}\left(x\right),\cdots,1_{A_{m}}\left(x\right)\right)$
est injective.

Donc $\text{card}\left(E\right)\leqslant\text{card}\left(\left\{0,1\right\} ^{m}\right)$ , c’est-à-dire $n\leqslant2^{m}$ .

Vu que $m$ est entier, cette dernière inégalité équivaut à :

$\boxed{m\geqslant\left\lceil \log_{2}\left(n\right)\right\rceil}$

Afin de montrer que cette minoration de $m$ est optimale, utilisons le théorème donnant l’existence et l’unicité, pour un entier naturel non nul, de son écriture en base 2.

Si nécessaire, consulter les vidéos Système de numération – 1 et Système de numération – 2, où cette question est étudiée en détail.

Afin de simplifier la présentation, supposons que $n=2^{p}$ pour un certain $p\in\mathbb{N}$ . Ce qui suit pourrait être adapté si $n$ n’est pas une puissance de 2.

On peut considérer, sans perte de généralité, que : $E=\llbracket0,2^{p}-1\rrbracket$ .

Chaque entier $k\in E$ possède une écriture binaire, de la forme :

$k=\sum_{i=0}^{p-1}b_{i}\left(k\right)\thinspace2^{i}$

avec $b_{i}\left(k\right)\in\left\{0,1\right\}$ pour tout $i$ .

Considérons alors, pour tout $i\in\llbracket0,p-1\rrbracket,$ l’ensemble :

$A_{i}=\left\{k\in E;\thinspace b_{i}\left(k\right)=1\right\}$

Alors $A_{0},\cdots,A_{p-1}$ sont des parties distinctes de $E.$ En effet, si $0\leqslant i,j\leqslant p-1$ et $i\neq j,$ alors $2^{i}\in A_{i}$ mais $2^{i}\notin A_{j},$ donc $A_{i}\neq A_{j}.$

En outre, étant donnés deux entiers $k\neq k'$ dans $\llbracket0,2^{p}-1\right\rrbracket,$ leurs écritures binaires diffèrent, donc il existe $i\in\llbracket0,p-1\rrbracket$ tel que $b_{i}\left(k\right)\neq b_{i}\left(k'\right).$ Autrement dit :

$\displaystyle{\exists i\in\llbracket0,p-1\rrbracket;\thinspace\begin{array}{cc}\mid & k\in A_{i}\text{ et }k'\notin A_{i}\\\text{ou}\\\mid & k\notin A_{i}\text{ et }k'\in A_{i}\end{array}}$

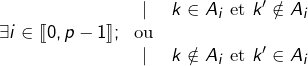
On a construit une famille de $p=\left\lceil \log_{2}\left(n\right)\right\rceil$ parties de $E$ possédant la propriété voulue.

Pour consulter l’énoncé, c’est ici

Partager cet article

Laisser un commentaire Annuler la réponse