Solution pour le challenge 31
Pour ![]() l’inégalité est évidente (et sans intérêt).
l’inégalité est évidente (et sans intérêt).
Supposons ![]() et (quitte à modifier l’indexation) que :
et (quitte à modifier l’indexation) que :
![]()
![Rendered by QuickLaTeX.com \[ \sum_{i=1}^{k}n_{i}^{2}=\left(n-k+1\right)^{2}+k-1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0fa164ac760bd5cbd096126c273b4080_l3.png)
Il reste à montrer que la valeur de la somme est moindre dans tous les autres cas.
Faisons donc l’hypothèse :
![]()
L’idée est de « déplacer une unité » vers le premier terme, en remplaçant :
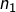 par
par 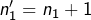
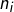 par
par 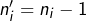
et en laissant inchangés les autres termes. La somme des ![]() n’est pas modifiée : sa valeur est encore
n’est pas modifiée : sa valeur est encore ![]() Quant à la somme des carrés, elle est remplacée par :
Quant à la somme des carrés, elle est remplacée par :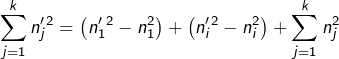
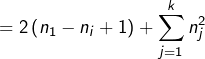
Or ![]() et donc :
et donc :
![Rendered by QuickLaTeX.com \[ \sum_{j=1}^{k}n_{j}^{2}<\sum_{j=1}^{k}n'_{j}^{2} \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-35e01758aea16dcf03c7b4a3a9ff01cc_l3.png)
Ceci prouve que la somme maximale est atteinte lorsque « toutes les unités ont été déplacées vers le premier terme », autrement dit dans le cas de figure ![]()
Pour consulter l’énoncé, c’est ici

