Solution pour le challenge 3
Il faut penser à utiliser les nombres complexes ! Posons dans toute la suite :
![]()
![]()
![]()
D’après la formule de Moivre :
![]()
Le but du jeu est de calculer la partie imaginaire de ![]() .
.
Or, l’expression qui définit ![]() est un fragment de la somme géométrique suivante :
est un fragment de la somme géométrique suivante :![]()
et cette somme vaut :
![]()
![]()
L’étape suivante consiste à observer que la somme et le produit de ![]() et
et ![]() sont aisément calculables. En effet :
sont aisément calculables. En effet :
![]()
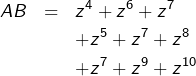
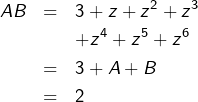
![Rendered by QuickLaTeX.com \[\boxed{\left\{\begin{array}{ccc}A+B & = & -1\\AB & = & 2\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9d97078ba263715febebcd0e8ae3ac19_l3.png)
![]()
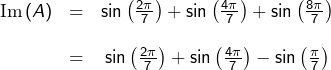
Or, d’une part :
![]()
![]()
![]()
En définitive :
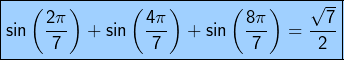
Pour consulter l’énoncé, c’est ici

