Solution pour le challenge n° 23

Solution pour le challenge 23

Commençons par observer que :

$(\spadesuit)$ Si trois entiers (ou plus) ont pour produit 1 ou -1, alors deux d’entre eux sont égaux.

Cette remarque est une simple conséquence du principe des tiroirs , vu qu’on a (au moins) trois facteurs et que chacun d’eux ne peut valoir que -1 ou 1.

Cela dit, il existe par hypothèse $R\in\mathbb{Z}\left[X\right]$ tel que :

$P-5=\left(X-a\right)\left(X-b\right)\left(X-c\right)\left(X-d\right)R$

Il s’agit de montrer qu’il n’existe aucun entier $k$ pour lequel :

$\left(k-a\right)\left(k-b\right)\left(k-c\right)\left(k-d\right)R\left(k\right)=3$

Supposons l’existence d’un tel $k$ et notons :

$\begin{eqnarray*}A&=&k-a\\B&=&k-b\\C&=&k-c\\D&=&k-d\end{eqnarray*}$

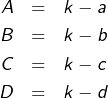
Comme 3 est premier, deux cas se présentent :

1er cas : $R\left(k\right)=\pm3$ .

Alors $ABCD=\pm1.$

D’après $\spadesuit$ , deux des quatre entiers $A,B,C,D$ sont égaux : absurde.

2ème cas : $R\left(k\right)=\pm1$ .

Alors l’un des quatre entiers $A,B,C$ ou $D$ vaut $\pm3,$ donc le produit des trois autres vaut $\pm1,$ et deux d’entre eux sont égaux d’après $\spadesuit$ : nouvelle contradiction .

Remarque

En remplaçant 4 par 3, on perd la conclusion.

Il existe en effet $P\in\mathbb{Z}\left[X\right]$ prenant trois fois la valeur 5 et prenant aussi la valeur 8 (chaque fois en des entiers). Par exemple : $P=5+\left(X+1\right)\left(X-1\right)\left(X-3\right)$
Manifestement :

$P(-1)=P(1)=P(3)=5$

$P(0)=8$

Pour consulter l’énoncé, c’est ici

Partager cet article

Remarque

Laisser un commentaire Annuler la réponse