Solution pour le challenge 22
Notons, pour tout ![]() et pour tout ensemble
et pour tout ensemble ![]() de cardinal
de cardinal ![]() :
:
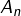 le nombre de parties de
le nombre de parties de 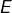 de cardinal congru à 0 modulo 3
de cardinal congru à 0 modulo 3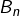 le nombre de parties de
le nombre de parties de 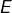 de cardinal congru à 1 modulo 3
de cardinal congru à 1 modulo 3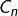 le nombre de parties de
le nombre de parties de 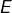 de cardinal congru à 2 modulo 3
de cardinal congru à 2 modulo 3
Comme le nombre de parties de ![]() de cardinal
de cardinal ![]() est égal à
est égal à ![]() alors :
alors :![]()
sachant que cette somme doit se poursuivre « tant que c’est possible », ce qui veut dire qu’on ajoute les entiers ![]() tant que
tant que ![]() . Bref :
. Bref :
![Rendered by QuickLaTeX.com \[\boxed{A_{n}=\sum_{k=0}^{\left\lfloor n/3\right\rfloor }\binom{n}{3k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-83de6f394158274d066177f1ce2dd158_l3.png)
![Rendered by QuickLaTeX.com \[B_{n}=\sum_{k=0}^{\left\lfloor (n-1)/3\right\rfloor }\binom{n}{3k+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a635abdb22ac58c051b6a35ff3056b24_l3.png)
![Rendered by QuickLaTeX.com \[C_{n}=\sum_{k=0}^{\left\lfloor (n-2)/3\right\rfloor }\binom{n}{3k+2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c72f4f7f21d47ab3e277b1a26f2b66bb_l3.png)
On fait intervenir le nombre complexe :
![]()
En effet, d’après la formule de Moivre :
![]()
On observe en outre que :![]()
Maintenant, appliquons la formule du binôme :
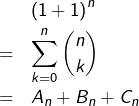
On a simplement séparé les
Compte tenu de ce qui a été dit au sujet du nombre complexe ![]() on dispose de deux égalités supplémentaires :
on dispose de deux égalités supplémentaires :
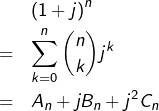
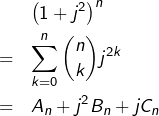
Nous disposons donc des trois relations suivantes :![]()
![]()
![]()
En les ajoutant membre à membre, et en tenant compte de ![]() il vient :
il vient :
![]()
Or, ![]() et
et ![]() sont conjugués et, par conséquent,
sont conjugués et, par conséquent, ![]() et
et ![]() sont aussi conjugués. Ceci conduit à :
sont aussi conjugués. Ceci conduit à :
![Rendered by QuickLaTeX.com \boxed{\displaystyle{A_{n}=\frac{1}{3}\left[2^{n}+2\thinspace\text{Re}\left(\left(1+j\right)^{n}\right)\right]}}](https://math-os.com/wp-content/ql-cache/quicklatex.com-bc974fd9522cc6f9dacced0906c1a7fb_l3.png)
Voilà déjà une formule explicite pour ![]() mais elle est un peu « compliquée ». On sait bien que
mais elle est un peu « compliquée ». On sait bien que ![]() est un entier naturel et l’on préférerait disposer d’une formule plus simple.
est un entier naturel et l’on préférerait disposer d’une formule plus simple.
Pour cela, on va tâcher de faire disparaître toute référence aux nombres complexes et à la trigonométrie…
On observe que, pour tout ![]() :
:
![]()
d’où, en passant aux parties réelles :
![]()
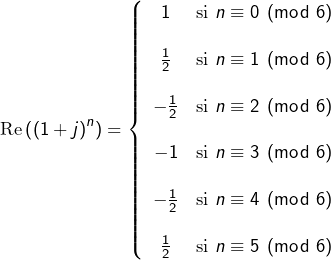
Finalement :
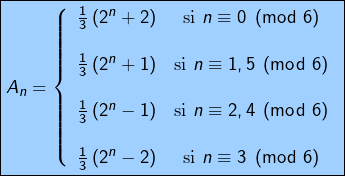
Passons à l’examen de la parité de ![]() Cette question ne semble pas facile d’accès avec la formule explicite obtenue ci-dessus.
Cette question ne semble pas facile d’accès avec la formule explicite obtenue ci-dessus.
Pourtant, en rédigeant un programme de calcul de ![]() (voir en annexe pour une version écrite en Python) et en observant la parité de
(voir en annexe pour une version écrite en Python) et en observant la parité de ![]() pour de petites valeurs de
pour de petites valeurs de ![]() on découvre une apparente régularité
on découvre une apparente régularité
1, 1, 1, 2, 5, 11, 22, 43, 85, 170, 341, 683, 1366, 2731, 5461, 10922, …
Pour ![]() , les
, les ![]() pairs sont
pairs sont ![]()
![]()
![]()
![]() et
et ![]()
On est donc naturellement conduit à la …
Conjecture
Pour tout entier ![]() :
:
![]()
ce qu’on va maintenant tâcher d’établir rigoureusement.
Pour cela, on va faire un petit raisonnement combinatoire.
Considérons un ensemble ![]() de cardinal
de cardinal ![]() et nommons
et nommons ![]() un élément particulier de
un élément particulier de ![]() . Les parties de
. Les parties de ![]() dont le cardinal est multiple de
dont le cardinal est multiple de ![]() sont :
sont :
- les parties de
 de cardinal multiple de
de cardinal multiple de 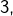
- les unions du singleton
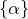 et d’une partie de
et d’une partie de 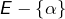 de cardinal congru à 2 modulo 3
de cardinal congru à 2 modulo 3
Par conséquent :![]()
Considérons maintenant un ensemble de cardinal ![]() et nommons
et nommons ![]() deux éléments particuliers. Les parties de
deux éléments particuliers. Les parties de ![]() dont le cardinal est multiple de 3 sont :
dont le cardinal est multiple de 3 sont :
- les parties de
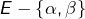 de cardinal multiple de
de cardinal multiple de 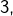
- les unions de l’un des deux singletons
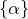 ou
ou 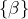 et d’une partie de
et d’une partie de 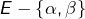 de cardinal congru à 2 modulo 3
de cardinal congru à 2 modulo 3 - les unions de la paire
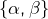 et d’une partie de
et d’une partie de 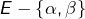 de cardinal congru à 1 modulo 3
de cardinal congru à 1 modulo 3
Par conséquent :![]()
Considérons enfin un ensemble de cardinal ![]() et nommons
et nommons ![]() trois éléments particuliers. Les parties de
trois éléments particuliers. Les parties de ![]() dont le cardinal est multiple de 3 sont :
dont le cardinal est multiple de 3 sont :
- les parties de
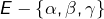 de cardinal multiple de
de cardinal multiple de 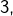
- les unions de l’un des trois singletons
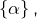
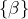 ou
ou 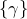 et d’une partie de
et d’une partie de 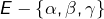 de cardinal congru à 2 modulo 3
de cardinal congru à 2 modulo 3 - les unions de l’une des trois paires
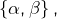
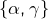 ou
ou 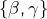 et d’une partie de
et d’une partie de 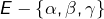 de cardinal congru à 1 modulo 3
de cardinal congru à 1 modulo 3 - l’union de
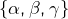 et d’une partie de
et d’une partie de 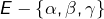 de cardinal multiple de 3
de cardinal multiple de 3
Par conséquent :![]()
En combinant ![]()
![]() et
et ![]() on obtient la relation de récurrence linéaire d’ordre 3 suivante :
on obtient la relation de récurrence linéaire d’ordre 3 suivante :![]()
Notons désormais :
![]()
![]()
1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, …
On peut aisément montrer par récurrence que, pour tout ![]() :
:
![]()
Annexe : programmation en Python
Calcul des coefficients binomiaux (solution récursive, utilisant la formule du pion)
def binomial(n,k):
if k == 0:
return 1
elif 2 * k > n:
return binomial(n, n-k)
else:
return (n * binomial(n-1,k-1)) // k
Calcul de la somme 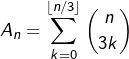
def A(n):
s = 0
k = 0
while k <= n:
s += binomial(n, k)
k += 3
return s
Pour consulter l’énoncé, c’est ici

