icone-challenge-math-OS

Solution pour la challenge 12

Posons pour tout n\in\mathbb{N} :

    \[u_{n}=a^{n}+b^{n}\]

Clairement, u_{0}\in\mathbb{N} et u_{1}\in\mathbb{N}.

Par ailleurs, pour tout n\in\mathbb{N}^{\star} :
u_{n+1}=a^{n+1}+b^{n+1}
=\left(a+b\right)\left(a^{n}+b^{n}\right)-ab\left(a^{n-1}+b^{n-1}\right)
=\left(a+b\right)u_{n}-ab\,u_{n-1}

Supposons que, pour un certain n\geqslant1, les réels u_{n-1} et u_{n} soient des entiers. On voit avec l’égalité ci-dessus que c’est aussi le cas de u_{n+1}.

On a montré par récurrence (d’ordre 2) que :

    \[\boxed{\forall n\in\mathbb{N},\thinspace u_{n}\in\mathbb{Z}}\]

Remarque

Etant donnés deux réels a,b, il n’est pas nécessaire que a et b soient entiers pour que a+b et ab le soient.

Par exemple :

    \begin{eqnarray*}a & = & 1+\sqrt{2}\\&\text{et}&\\b & = & 1-\sqrt{2}\end{eqnarray*}

Bien sûr, si a+b\in\mathbb{Z} et si l’un des deux nombres a ou b est entier, alors l’autre aussi comme différence de deux entiers !

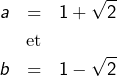
Pour consulter l’énoncé, c’est ici

Partager cet article
    

Laisser un commentaire