Solution pour le challenge 1
Méthode 1
➣ Si ![]() et
et ![]() , alors :
, alors :
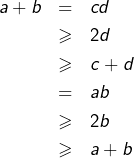
En particulier : ![]() c’est-à-dire
c’est-à-dire ![]() ce qui impose
ce qui impose ![]()
De la même façon ![]() Bref :
Bref : ![]()
➣ Supposons maintenant le contraire, c’est-à-dire : ![]() ou
ou ![]()
Si ![]() alors par hypothèse :
alors par hypothèse :
![]()
Vu que ![]() il s’ensuit que
il s’ensuit que ![]() et
et ![]() d’où
d’où ![]()
Ainsi ![]()
Et si ![]() on parvient de même à
on parvient de même à ![]()
En conclusion, il existe trois quadruplets solutions :
![Rendered by QuickLaTeX.com \[\boxed{\begin{matrix}t_1&=&\left(2,2,2,2\right)\\t_2&=&\left(1,5,2,3\right)\\t_3&=&\left(2,3,1,5\right)\end{matrix}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9b265126a3f3f492e7e12964587df22a_l3.png)
Méthode 2
On observe que :
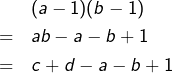
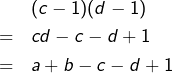
Trois cas se présentent :
➣ Cas 1 :
![]()
![]()
➣ Cas 2 :
![]()
➣ Cas 3 :
![]()
On retrouve les trois couples solutions obtenus par la méthode 1.
Pour consulter l’énoncé, c’est ici
Partager cet article

