Question
Il me semble qu’une fonction qui n’est pas croissante devait être décroissante !
Pourtant on m’ a dit que c’est faux. Pouvez-vous m’éclairer ?
Réponse
Le vocabulaire mathématique est généralement très bien conçu.
Cependant il arrive, dans un petit nombre de cas, que la terminologie standard heurte quelque peu notre sens commun.
On pourrait s’attendre à ce que les préfixes ‘in- » (ou « im-« ) et « dé- » annoncent la négation de quelque chose. C’est d’ailleurs parfois le cas : un entier « impair » est un entier qui n’est pas pair.
Mais pas toujours … dire qu’une fonction est « impaire » ne signifie pas qu’elle n’est pas paire. La fonction ![]() n’est en effet ni paire ni impaire. Quant à la fonction nulle, elle est simultanément paire et impaire (mais c’est la seule dans ce cas…) !
n’est en effet ni paire ni impaire. Quant à la fonction nulle, elle est simultanément paire et impaire (mais c’est la seule dans ce cas…) !
De la même manière, lorsqu’une fonction est qualifiée de « décroissante », cela ne signifie pas qu’elle n’est pas croissante.
Etant donnée une fonction ![]() on dit que
on dit que ![]() est croissante lorsque :
est croissante lorsque :
![]()
ce qui signifie que ![]() préserve l’ordre entre les nombres réels. Si un réel est plus petit qu’un autre, l’image du premier sera inférieure (ou égale) à l’image du second.
préserve l’ordre entre les nombres réels. Si un réel est plus petit qu’un autre, l’image du premier sera inférieure (ou égale) à l’image du second.
On dit que ![]() est décroissante lorsque :
est décroissante lorsque :
![]()
Cette fois, ![]() renverse l’ordre entre les réels. Si un réel est plus petit qu’un autre, l’image du premier sera supérieure (ou égale) à l’image du second.
renverse l’ordre entre les réels. Si un réel est plus petit qu’un autre, l’image du premier sera supérieure (ou égale) à l’image du second.
Il n’est pas difficile de trouver une fonction qui ne soit ni croissante, ni décroissante. Par exemple, celle définie par :
![]()
En effet :
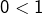 mais
mais 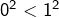 ce qui prouve que
ce qui prouve que  n’est pas décroissante
n’est pas décroissante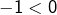 mais
mais 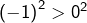 ce qui prouve que
ce qui prouve que  n’est pas croissante non plus.
n’est pas croissante non plus.

