Ce qui suit est une mise en forme d’une démonstration écrite par Levi Ben Gerson en 1343 à la demande de Philippe de Vitry (voir la dernière section de l’article Qu’est-ce qu’une conjecture pour plus de détails).
Les connaissances requises sont quelques notions élémentaires d’algèbre et d’arithmétique.
Le résultat démontré ici est une version très rudimentaire de la conjecture de Catalan, selon laquelle les entiers 8 et 9 constituent le seul couple de puissances parfaites consécutives.
Enoncé
On appelle « nombre harmonique » tout entier de la forme ![]() où
où ![]()
On se propose de montrer que les seules paires de nombres harmoniques consécutifs sont ![]() ,
, ![]() ,
, ![]() et
et ![]()
On considère donc deux entiers ![]() définis par :
définis par :
![]()
- Montrer que
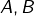 ne peuvent pas être tous deux pairs.
ne peuvent pas être tous deux pairs. - Montrer que
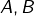 ne peuvent pas être tous deux multiples de
ne peuvent pas être tous deux multiples de 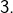
- On suppose donc maintenant que
 et
et 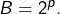
- Montrer que
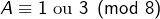
- Montrer que si
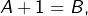 alors
alors 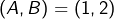 ou
ou 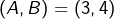
- Montrer que si
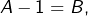 alors
alors 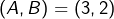 ou
ou 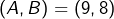
- Montrer que
Solution
- Si
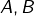 sont tous deux pairs, alors (comme
sont tous deux pairs, alors (comme 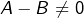 ) :
) :
… contradiction.![Rendered by QuickLaTeX.com \[\left|A-B\right|\geqslant2\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0202be8a341d3a4692261aeac4acc597_l3.png)
- De même, si
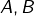 sont tous deux multiples de
sont tous deux multiples de 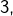 alors (comme
alors (comme 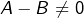 ) :
) :
… nouvelle contradiction.![Rendered by QuickLaTeX.com \[\left|A-B\right|\geqslant3\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5f3609a780479ae667ae4fbf058fceae_l3.png)
- Comme
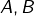 ne sont ni simultanément pairs, ni simultanément multiples de 3, on peut supposer que l’un deux est une puissance de 2 et que l’autre est une puissance de 3. Posons donc :
ne sont ni simultanément pairs, ni simultanément multiples de 3, on peut supposer que l’un deux est une puissance de 2 et que l’autre est une puissance de 3. Posons donc :![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$A=3^{n}$}\qquad\text{et}\qquad\fcolorbox{black}{myBlue}{$B=2^{p}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-60e9ed4f386e15c491a3472b3c735a40_l3.png)
- Si n est pair, alors en posant
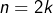 :
:
et sinon, en posant![Rendered by QuickLaTeX.com \[A=3^{2k}=9^{k}\equiv1\pmod{8}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ba84496d116d275e994d1bda07400058_l3.png)
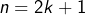 :
:![Rendered by QuickLaTeX.com \[A=3^{2k+1}=3\times9^{k}\equiv3\pmod{8}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-605ea861bb04ded9477c1fafdc388256_l3.png)
- Si
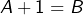 , alors
, alors 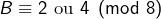 ce qui impose
ce qui impose 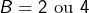 et donc :
et donc :![Rendered by QuickLaTeX.com \[\left(A,B\right)=\left(1,2\right)\text{ ou }\left(A,B\right)=\left(3,4\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a46316dd62953e4d35bdab7c8db8eaaa_l3.png)
- Si
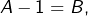 alors
alors 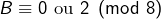 c’est-à-dire :
c’est-à-dire :
Si![Rendered by QuickLaTeX.com \[B=2\text{ ou }\left(B=2^{p}\text{ avec }p\geqslant3\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d1a7bf7ebf49935b1a877883f4e340d5_l3.png)
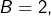 alors
alors 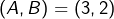 et sinon,
et sinon,  est nécessairement pair (d’après 3-a). En posant
est nécessairement pair (d’après 3-a). En posant 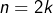 , la relation
, la relation 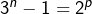 prend la forme :
prend la forme :
ce qui montre que![Rendered by QuickLaTeX.com \[\left(3^{k}-1\right)\left(3^{k}+1\right)=2^{p}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d3adb16ee22428fd99c15e0236b43d9b_l3.png)
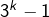 et
et 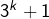 sont deux puissances de
sont deux puissances de 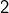 distantes de
distantes de 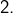 Il ne peut s’agir que de
Il ne peut s’agir que de 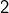 et
et 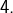 Bref :
Bref : 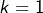 et donc
et donc ![Rendered by QuickLaTeX.com \[\left(A,B\right)=\left(9,8\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-09ad3044f1866937c3a8d0bddde42a0e_l3.png)
- Si n est pair, alors en posant
