Lettre S
SÉRIE
A toute suite ![]() de nombres complexes, on peut associer la suite
de nombres complexes, on peut associer la suite ![]() des sommes partielles, en posant pour tout
des sommes partielles, en posant pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[ S_{n}=\sum_{k=0}^{n}u_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9259f5581a34fd53baf4c2766b84b754_l3.png)
Cette définition fait sens puisque, connaissant ![]() on retrouve aussitôt
on retrouve aussitôt ![]() en calculant :
en calculant :
![]()
![]()
Toujours en cas de convergence, on définit le reste de rang ![]() comme étant :
comme étant :
![Rendered by QuickLaTeX.com \[R_{n}=\sum_{k=0}^{\infty}u_{k}-\sum_{k=0}^{n}u_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7a75aa519c5376214b7527a9836a81a4_l3.png)
![]()
Remarque
La notion de série convergente s’étudie plus généralement dans le cadre des espaces vectoriels normés.
Exemple 1
Si ![]() est tel que
est tel que ![]() alors la série géométrique
alors la série géométrique ![]() converge et sa somme est :
converge et sa somme est :
![Rendered by QuickLaTeX.com \[\sum_{k=0}^{\infty}q^{k}=\frac{1}{1-q}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9666821c90713d3c9c646abb747f108c_l3.png)
Exemple 2
Si ![]() le développement décimal propre de
le développement décimal propre de ![]() n’est autre que l’écriture de
n’est autre que l’écriture de ![]() comme somme d’une série particulière :
comme somme d’une série particulière :
![Rendered by QuickLaTeX.com \[x=\sum_{k=1}^{\infty}c_{k}\left(x\right)\thinspace10^{-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-203bd8a57db8c5bd1ac3e9911f0b71b6_l3.png)
![]()
![]()
![]()
![]()
Exemple 3
Si ![]() est tel que
est tel que ![]() alors la série de Riemann
alors la série de Riemann 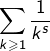 converge et sa somme est notée
converge et sa somme est notée ![]()
La fonction ![]() ainsi définie est appelée fonction zeta de Riemann. On peut montrer que, pour tout entier
ainsi définie est appelée fonction zeta de Riemann. On peut montrer que, pour tout entier ![]() :
:
![]()
![]()
Si une série converge, alors son terme général tend vers 0 et la réciproque est fausse, comme on le voit avec la série harmonique :
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}\sum_{k=1}^{n}\frac{1}{k} & \geqslant & \sum_{k=1}^{n}\ln\left(1+\frac{1}{k}\right)\\ & = & \sum_{k=1}^{n}\left[\ln\left(k+1\right)-\ln\left(k\right)\right]\\ & = & \ln\left(n+1\right) \end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-c916932fd6818075779050b78b201e86_l3.png)
L’étude de la nature (convergence ou divergence) d’une série se fait habituellement au moyen d’un cortège de régles (conditions nécessaires ou suffisantes de convergence), comme par exemple la règle de d’Alembert, la théorème des séries alternées ou encore de le théorème de convergence absolue.
Cependant, l’ensemble des règles connues ne suffit pas à traiter n’importe quel exemple …
Exemple 4
La nature de la série
![Rendered by QuickLaTeX.com \[\sum_{k\geqslant1}\frac{1}{k^{2}\sin\left(k\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d09bf8b6afcd94dbe862e7a22ac436f2_l3.png)
SUITE
Soit ![]() un ensemble non vide.
un ensemble non vide.
Une suite à termes dans ![]() est une application
est une application ![]() .
.
Si ![]() est une suite, on note
est une suite, on note ![]() son terme de rang
son terme de rang ![]() (on dit aussi : d‘indice
(on dit aussi : d‘indice ![]() ); c’est l’image de
); c’est l’image de ![]() par l’application
par l’application ![]() . Cette notation, largement utilisée, est une alternative à la notation
. Cette notation, largement utilisée, est une alternative à la notation ![]() , qu’on utilise habituellement pour désigner l’image d’un élément par une application.
, qu’on utilise habituellement pour désigner l’image d’un élément par une application.
Si l’on dispose d’une formule pour ![]() , on peut alors noter
, on peut alors noter ![]() au lieu de
au lieu de ![]() .
.
Par exemple : la suite ![]() .
.
Par extension, l’ensemble de départ d’une suite n’est pas obligatoirement ![]() . Il peut s’agir, plus généralement, d’une partie de
. Il peut s’agir, plus généralement, d’une partie de ![]() de la forme
de la forme ![]() , pour un certain
, pour un certain ![]() .
.
On note alors ![]() . Par exemple : la suite
. Par exemple : la suite ![]() .
.
Attention ! Ne pas confondre :
- la suite
 à termes dans
à termes dans 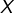 : c’est une application de
: c’est une application de 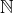 dans
dans 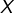 .
. - le terme
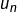 : c’est un élément de
: c’est un élément de 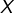 .
. - l’ensemble
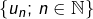 des termes de la suite
des termes de la suite  : c’est une partie de
: c’est une partie de 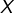 .
.

