Lettre N
(élément) NEUTRE
Etant donnée une opération ![]() sur un ensemble
sur un ensemble ![]() , un élément
, un élément ![]() est dit neutre à gauche pour cette opération lorsque :
est dit neutre à gauche pour cette opération lorsque :
![]()
On définit de même la notion d’élément neutre à droite. Un élément neutre (tout court) est un élément à la fois neutre à gauche et neutre à droite. Ces trois notions se confondent si ![]() est commutative.
est commutative.
L’existence d’un élément neutre n’est pas garantie (voir exemple plus bas).
En revanche, il y a unicité puisque si ![]() et
et ![]() sont neutres pour
sont neutres pour ![]() , alors :
, alors :
![]()
Quelques exemples usuels :
- Le neutre pour l’addition dans
 est 0.
est 0. - Le neutre pour la multiplication dans
 est 1.
est 1. - Le neutre pour la composition (loi
 ) dans
) dans 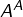 (ensemble des applications de
(ensemble des applications de 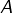 dans lui-même) est l’application identité
dans lui-même) est l’application identité 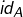 .
. - Les neutres des opérations d’union et d’intersection dans
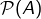 (ensemble des parties de
(ensemble des parties de 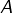 ) sont respectivement
) sont respectivement 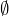 et
et 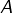 .
. - Le neutre de la multiplication dans
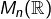 est la matrice unité
est la matrice unité 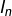 .
.
Pour la soustraction dans ![]() , il n’existe pas d’élément neutre (toutefois, 0 est neutre à droite).
, il n’existe pas d’élément neutre (toutefois, 0 est neutre à droite).
NORME
Etant donné un ![]() espace vectoriel
espace vectoriel ![]() une norme sur
une norme sur ![]() est une application
est une application ![]() vérifiant les trois conditions suivantes :
vérifiant les trois conditions suivantes :
- Homogénéité :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\forall\left(\lambda,x\right)\in\mathbb{R}\times E,\thinspace N\left(\lambda x\right)=\left|\lambda\right|\thinspace N\left(x\right)$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b6b90be8376525c15de63c79cdfb13f3_l3.png)
- Inégalité triangulaire :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\forall\left(x,y\right)\in E^{2},\thinspace N\left(x+y\right)\leqslant N\left(x\right)+N\left(y\right)$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f2c7e49821a7c091ca474d41966453ab_l3.png)
- Condition de séparation :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\forall x\in E,\thinspace N\left(x\right)=0\Rightarrow x=0_{E}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-70f9d3a22b556385977ded050fca1c60_l3.png)
On peut définir de la même façon une norme sur un ![]() espace vectoriel, en considérant bien sûr que
espace vectoriel, en considérant bien sûr que ![]() désigne cette fois le module du nombre complexe
désigne cette fois le module du nombre complexe ![]()
Un ![]() ev muni d’une norme est un espace vectoriel normé (evn en abrégé).
ev muni d’une norme est un espace vectoriel normé (evn en abrégé).
On définit, pour ![]() et
et ![]() la boule ouverte de centre
la boule ouverte de centre ![]() et de rayon
et de rayon ![]() :
:
![]()
L’application :
![]()
Exemples fondamentaux
➣ Dans ![]() les trois normes standard sont définies par :
les trois normes standard sont définies par :
![Rendered by QuickLaTeX.com \[ \forall x\in\mathbb{R}^{n},\thinspace\left\{ \begin{array}{ccc} N_{1}\left(x\right) & = & {\displaystyle \sum_{i=1}^{n}\left|x_{i}\right|}\\ \\ N_{2}\left(x\right) & = & {\displaystyle \left(\sum_{i=1}^{n}x_{i}^{2}\right)^{1/2}}\\ \\ N_{\infty}\left(x\right) & = & {\displaystyle \max_{1\leqslant i\leqslant n}\left|x_{i}\right|} \end{array}\right. \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2666cb8a04d731c1a0fe8f52e1b2821e_l3.png)
On notera que si ![]() , ces trois normes se confondent : on retrouve la valeur absolue (qui est la norme usuelle sur
, ces trois normes se confondent : on retrouve la valeur absolue (qui est la norme usuelle sur ![]() ).
).
➣ Dans l’espace ![]() des applications continues de
des applications continues de ![]() dans
dans ![]() les trois normes standard sont définies par :
les trois normes standard sont définies par :
![Rendered by QuickLaTeX.com \[\forall f\in\mathcal{C}\left(\left[a,b\right],\mathbb{R}\right),\thinspace\left\{ \begin{array}{ccc} \left\Vert f\right\Vert_{1} & = & {\displaystyle \int_{a}^{b}\left|f\left(t\right)\right|\thinspace dt}\\\\\left\Vert f\right\Vert_{2} & = & {\displaystyle \left(\int_{a}^{b}f\left(t\right)^{2}\thinspace dt\right)^{1/2}}\\\\\left\Vert f\right\Vert_{\infty} & = & {\displaystyle \sup_{t\in\left[a,b\right]}\left|f\left(t\right)\right|}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-83d30c87e2f623b1952f6b9906ed1557_l3.png)
Normes euclidiennes
Si un ![]() espace vectoriel
espace vectoriel ![]() est muni d’un produit scalaire, alors l’application :
est muni d’un produit scalaire, alors l’application :
![]()
Dans les exemples ci-dessus :
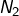 est une norme euclidienne sur
est une norme euclidienne sur 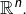 Elle est issue du produit scalaire défini par :
Elle est issue du produit scalaire défini par :![Rendered by QuickLaTeX.com \[\left(x\mid y\right)=\sum_{i=1}^{n}x_{i}y_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c157678f859f0182830e6ff62ae07e28_l3.png)
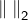 est une norme euclidienne sur
est une norme euclidienne sur ![Rendered by QuickLaTeX.com \mathcal{C}\left(\left[a,b\right],\mathbb{R}\right).](https://math-os.com/wp-content/ql-cache/quicklatex.com-1b92b6d8f0ccc32cad85945362a6509c_l3.png) Elle est issue du produit scalaire défini par :
Elle est issue du produit scalaire défini par :![Rendered by QuickLaTeX.com \[\left(f\mid g\right)=\int_{a}^{b}f\left(t\right)\thinspace g\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0786232c40dc02b7e5825dfa791d09b0_l3.png)
Une condition nécessaire et suffisante pour qu’une norme ![]() sur un
sur un ![]() espace vectoriel
espace vectoriel ![]() soit euclidienne est qu’elle vérifie la formule du parallélogramme :
soit euclidienne est qu’elle vérifie la formule du parallélogramme :
![]()
Signalons encore un résultat important (parmi tant d’autres) :
Etant donné un ![]() espace vectoriel
espace vectoriel ![]() une norme sur
une norme sur ![]() est une application
est une application ![]() vérifiant les trois conditions suivantes :
vérifiant les trois conditions suivantes :
- Homogénéité :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\forall\left(\lambda,x\right)\in\mathbb{R}\times E,\thinspace N\left(\lambda x\right)=\left|\lambda\right|\thinspace N\left(x\right)$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b6b90be8376525c15de63c79cdfb13f3_l3.png)
- Inégalité triangulaire :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\forall\left(x,y\right)\in E^{2},\thinspace N\left(x+y\right)\leqslant N\left(x\right)+N\left(y\right)$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f2c7e49821a7c091ca474d41966453ab_l3.png)
- Condition de séparation :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\forall x\in E,\thinspace N\left(x\right)=0\Rightarrow x=0_{E}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-70f9d3a22b556385977ded050fca1c60_l3.png)
On peut définir de la même façon une norme sur un ![]() espace vectoriel, en considérant bien sûr que
espace vectoriel, en considérant bien sûr que ![]() désigne cette fois le module du nombre complexe
désigne cette fois le module du nombre complexe ![]()
Un ![]() ev muni d’une norme est un espace vectoriel normé (evn en abrégé).
ev muni d’une norme est un espace vectoriel normé (evn en abrégé).
On définit, pour ![]() et
et ![]() la boule ouverte de centre
la boule ouverte de centre ![]() et de rayon
et de rayon ![]() :
:
![]()
L’application :
![]()
Exemples fondamentaux
➣ Dans ![]() les trois normes standard sont définies par :
les trois normes standard sont définies par :
![Rendered by QuickLaTeX.com \[ \forall x\in\mathbb{R}^{n},\thinspace\left\{ \begin{array}{ccc} N_{1}\left(x\right) & = & {\displaystyle \sum_{i=1}^{n}\left|x_{i}\right|}\\ \\ N_{2}\left(x\right) & = & {\displaystyle \left(\sum_{i=1}^{n}x_{i}^{2}\right)^{1/2}}\\ \\ N_{\infty}\left(x\right) & = & {\displaystyle \max_{1\leqslant i\leqslant n}\left|x_{i}\right|} \end{array}\right. \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2666cb8a04d731c1a0fe8f52e1b2821e_l3.png)
On notera que si ![]() , ces trois normes se confondent : on retrouve la valeur absolue (qui est la norme usuelle sur
, ces trois normes se confondent : on retrouve la valeur absolue (qui est la norme usuelle sur ![]() ).
).
➣ Dans l’espace ![]() des applications continues de
des applications continues de ![]() dans
dans ![]() les trois normes standard sont définies par :
les trois normes standard sont définies par :
![Rendered by QuickLaTeX.com \[\forall f\in\mathcal{C}\left(\left[a,b\right],\mathbb{R}\right),\thinspace\left\{ \begin{array}{ccc} \left\Vert f\right\Vert_{1} & = & {\displaystyle \int_{a}^{b}\left|f\left(t\right)\right|\thinspace dt}\\\\\left\Vert f\right\Vert_{2} & = & {\displaystyle \left(\int_{a}^{b}f\left(t\right)^{2}\thinspace dt\right)^{1/2}}\\\\\left\Vert f\right\Vert_{\infty} & = & {\displaystyle \sup_{t\in\left[a,b\right]}\left|f\left(t\right)\right|}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-83d30c87e2f623b1952f6b9906ed1557_l3.png)
Normes euclidiennes
Si un ![]() espace vectoriel
espace vectoriel ![]() est muni d’un produit scalaire, alors l’application :
est muni d’un produit scalaire, alors l’application :
![]()
Dans les exemples ci-dessus :
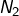 est une norme euclidienne sur
est une norme euclidienne sur 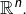 Elle est issue du produit scalaire défini par :
Elle est issue du produit scalaire défini par :![Rendered by QuickLaTeX.com \[\left(x\mid y\right)=\sum_{i=1}^{n}x_{i}y_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c157678f859f0182830e6ff62ae07e28_l3.png)
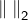 est une norme euclidienne sur
est une norme euclidienne sur ![Rendered by QuickLaTeX.com \mathcal{C}\left(\left[a,b\right],\mathbb{R}\right).](https://math-os.com/wp-content/ql-cache/quicklatex.com-1b92b6d8f0ccc32cad85945362a6509c_l3.png) Elle est issue du produit scalaire défini par :
Elle est issue du produit scalaire défini par :![Rendered by QuickLaTeX.com \[\left(f\mid g\right)=\int_{a}^{b}f\left(t\right)\thinspace g\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0786232c40dc02b7e5825dfa791d09b0_l3.png)
Une condition nécessaire et suffisante pour qu’une norme ![]() sur un
sur un ![]() espace vectoriel
espace vectoriel ![]() soit euclidienne est qu’elle vérifie la formule du parallélogramme :
soit euclidienne est qu’elle vérifie la formule du parallélogramme :
![]()
Signalons encore un résultat important (parmi tant d’autres) :
NOYAU
Considérons deux groupes ![]() et
et ![]()
On adopte la notation multiplicative pour l’un comme pour l’autre. En particulier, les éléments neutres sont respectivement notés ![]() et
et ![]()
Etant donné un morphisme de groupes ![]() le noyau de
le noyau de ![]() est par définition :
est par définition :
![]()
![]() est plus précisément un sous-groupe normal (distingué) de
est plus précisément un sous-groupe normal (distingué) de ![]() et le groupe quotient
et le groupe quotient ![]() est isomorphe au sous-groupe
est isomorphe au sous-groupe ![]() de
de ![]()
La notation ker provient de mots anglais kernel et allemand Kern, qui signifient noyau.
Exemple
L’application ![]() est un morphisme du groupe
est un morphisme du groupe ![]() vers le groupe
vers le groupe ![]() dont le noyau est
dont le noyau est ![]() Comme l’image directe de
Comme l’image directe de ![]() par ce morphisme est le groupe
par ce morphisme est le groupe ![]() des nombres complexes de module 1, il en résulte que les groupes
des nombres complexes de module 1, il en résulte que les groupes ![]() et
et ![]() sont isomorphes.
sont isomorphes.
➣ On définit le noyau d’un morphisme d’anneaux comme étant le noyau du morphisme des groupes additifs sous-jacents. En clair, si ![]() et
et ![]() sont des anneaux et si
sont des anneaux et si ![]() est un morphisme d’anneaux, alors par définition :
est un morphisme d’anneaux, alors par définition :
![]()
➣ De même, si ![]() est un corps et si
est un corps et si ![]() sont deux
sont deux ![]() espaces vectoriels, alors le noyau d’une application linéaire
espaces vectoriels, alors le noyau d’une application linéaire ![]() est :
est :
![]()
Le noyau d’une application linéaire est un sous-espace vectoriel de l’espace vectoriel de départ.
➣ En superposant, en quelque sorte, les deux points précédents, on obtient la notion de noyau d’un morphisme de ![]() -algèbres.
-algèbres.
Exemple
Etant donné un ![]() espace vectoriel
espace vectoriel ![]() ainsi qu’un endomorphisme
ainsi qu’un endomorphisme ![]() , l’application
, l’application
![]()
L’anneau ![]() étant principal, ceci entraîne que si
étant principal, ceci entraîne que si ![]() (ce qui est automatiquement le cas dès que
(ce qui est automatiquement le cas dès que ![]() est de dimension finie) alors il existe un (unique) polynôme unitaire
est de dimension finie) alors il existe un (unique) polynôme unitaire ![]() qui engendre cet idéal. C’est le fameux polynôme minimal annulateur de
qui engendre cet idéal. C’est le fameux polynôme minimal annulateur de ![]() dont on peut montrer que les racines dans
dont on peut montrer que les racines dans ![]() sont exactement les valeurs propres de
sont exactement les valeurs propres de ![]() et qui est un diviseur de tout polynôme annulateur de
et qui est un diviseur de tout polynôme annulateur de ![]() (et donc, notamment, de son polynôme caractéristique, d’après le théorème de Cayley-Hamilton).
(et donc, notamment, de son polynôme caractéristique, d’après le théorème de Cayley-Hamilton).

