Lettre L

LINÉARISATION (trigonométrie)

En trigonométrie circulaire, linéariser une expression consiste à « faire disparaître » les produits de sinus et / ou de cosinus. Plus précisément, étant donnée une fonction trigonométrique f, il s’agit (lorsque c’est possible) d’obtenir une expression du type :

    \[f\left(x\right)=\sum_{k=0}^{n}\left(a_{k}\cos\left(kx\right)+b_{k}\sin\left(kx\right)\right)\]

où les a_{k}et les b_{k} sont des constantes. Par exemple, connaissant la formule dite « de duplication du cosinus » :

    \[\cos\left(2x\right)=2\cos^{2}\left(x\right)-1\]

on obtient immédiatement :

    \[\boxed{\cos^{2}\left(x\right)=\dfrac{1+\cos\left(2x\right)}{2}}\]

qui est la formule de linéarisation de \cos^{2}\left(x\right). Et comme \cos^{2}\left(x\right)+\sin^{2}\left(x\right)=1, on en déduit la formule de linéarisation de \sin^{2}\left(x\right) :

    \[\boxed{\sin^{2}\left(x\right)=\dfrac{1-\cos\left(2x\right)}{2}}\]

On peut traiter de manière analogue le cas de l’exposant 3. En gros, en partant de la formule d’addition du cosinus :

    \[\cos\left(a+b\right)=\cos\left(a\right)\cos\left(b\right)-\sin\left(a\right)\sin\left(b\right)\]

puis en remplaçant a et b par 2x et x respectivement, on obtient assez vite la formule :

    \[\cos\left(3x\right)=4\cos^{3}\left(x\right)-3\cos\left(x\right)\]

d’où l’on tire la formule de linéarisation de \cos^{3}\left(x\right) :

    \[\boxed{\cos^{3}\left(x\right)=\dfrac{1}{4}\left(\cos\left(3x\right)+3\cos\left(x\right)\right)}\]

Un travail similaire, mais en partant cette fois de la formule d’addition du sinus :

    \[\sin\left(a+b\right)=\sin\left(a\right)\cos\left(b\right)+\cos\left(a\right)\sin\left(b\right)\]

conduit à :

    \[\boxed{\sin^{3}\left(x\right)=\dfrac{1}{4}\left(3\sin\left(x\right)-\sin\left(3x\right)\right)}\]

Pour aller plus loin dans cette direction, la bonne idée consiste à faire intervenir les nombres complexes. En posant :

    \[z=e^{ix}\]

et en observant que :

    \[\cos^{n}\left(x\right)=\left(\dfrac{z+\overline{z}}{2}\right)^{n}\qquad\text{et}\qquad\sin^{n}\left(x\right)=\left(\dfrac{z-\overline{z}}{2i}\right)^{n}\]

puis en développant ces expressions au moyen de la formule du binôme, on obtient quatre formules de linéarisation pour les puissances de \cos\left(x\right) ou de \sin\left(x\right) (quatre, car il s’avère que la parité de l’exposant n compte). Ces formules sont données ci-dessous, sans démonstration :

    \[\fcolorbox{black}{myBlue}{$\displaystyle{\cos^{2p+1}\left(x\right)=\frac{1}{4^{p}}\sum_{k=0}^{p}\binom{2p+1}{p-k}\cos\left(\left(2k+1\right)x\right)}$}\]


    \[\fcolorbox{black}{myBlue}{$\displaystyle{\cos^{2p}\left(x\right)=\frac{1}{4^{p}}\left[\binom{2p}{p}+2\sum_{k=1}^{p}\binom{2p}{p-k}\cos\left(2kx\right)\right]}$}\]


    \[\fcolorbox{black}{myBlue}{$\displaystyle{\sin^{2p+1}\left(x\right)=\frac{1}{4^{p}}\sum_{k=0}^{p}\left(-1\right)^{k}\binom{2p+1}{p-k}\sin\left(\left(2k+1\right)x\right)}$}\]


    \[\fcolorbox{black}{myBlue}{$\displaystyle{\sin^{2p}\left(x\right)=\frac{1}{4^{p}}\left[\binom{2p}{p}+2\sum_{k=1}^{p}\left(-1\right)^{k}\binom{2p}{p-k}\cos\left(2kx\right)\right]}$}\]

Ajoutons pour terminer que ces formules de linéarisation (et d’autres, similaires) donnent accès, par exemple, au calcul de certaines intégrales. Ainsi, on peut vérifier que :

    \[\int_0^{\pi/2}\sin^6(t)\,dt=\frac{5\pi}{32}\]

et (mais c’est nettement moins immédiat) que :

    \[\int_0^{+\infty}\frac{\sin^6(t)}{t^2}\,dt=\frac{3\pi}{16}\]

LIPSCHITZIENNE (application)

Définition

Considérons un intervalle non trivial I de \mathbb{R} et un réel k\geqslant0.

Une application f:I\rightarrow\mathbb{R} est dite \mathbf{k-}lipschitzienne lorsque :

(\star)   \[\forall\left(x,x'\right)\in I^{2},\thinspace\left|f\left(x\right)-f\left(x'\right)\right|\leqslant k\left|x-x'\right|\]

On dit que f est lipschitzienne, lorsqu’il existe k\geqslant0 tel que f soit k-lipschitzienne.

En notant \Gamma le graphe de f, la condition \left(\star\right) signifie que les pentes des cordes de \Gamma sont comprises entre -k et k. Autrement dit : une application est lipschitzienne lorsque l’ensemble des pentes de son graphe est majoré.

Proposition 1

Si f:I\rightarrow\mathbb{R} est dérivable, alors :

    \[f \text{ est lipschitzienne}\Leftrightarrow f'\text{ est bornée}\]

Dans un sens, c’est une conséquence directe de la formule des accroissements finis. Dans l’autre, il suffit d’écrire que les taux d’accroissements sont bornés et de passer à la limite.

Attention : une application lipschitzienne n’a aucune raison d’être dérivable ! Penser par exemple à la valeur absolue, qui n’est pas dérivable en 0, mais qui est 1-lipschitzienne puisque (inégalité triangulaire) :

    \[\forall\left(x,x'\right)\in\mathbb{R}^{2},\thinspace\left|\left|x\right|-\left|y\right|\right|\leqslant\left|x-y\right|\]

Proposition 2

Toute application lipschitzienne est uniformément continue.

C’est immédiat et la réciproque est fausse : l’application \left[0,+\infty\right[\rightarrow\mathbb{R},\thinspace x\mapsto\sqrt{x} est uniformément continue mais non lipschitzienne.

Exemple 1

L’application f:\mathbb{R}\rightarrow\mathbb{R},\thinspace x\mapsto\sin\left(x^{2}\right) n’est pas lipschitzienne puisqu’elle est dérivable et à dérivé non bornée. En effet, pour tout x\in\mathbb{R} :

    \[f'\left(x\right)=2x\cos\left(x^{2}\right)\]

En particulier, pour tout n\in\mathbb{N} :

    \[f'\left(\sqrt{2\pi n}\right)=2\sqrt{2\pi n}\]

et donc {\displaystyle \lim_{n\rightarrow\infty}f'\left(\sqrt{2\pi n}\right)=+\infty.}

Exemple 2

Etant données une application continue f:\left[0,1\right]\rightarrow\mathbb{R} et une application lipschitzienne \varphi:\mathbb{R}\rightarrow\mathbb{R}, posons pour tout x\in\mathbb{R} :

    \[F\left(x\right)=\int_{0}^{1}f\left(t\right)\varphi\left(xt\right)\thinspace dt\]

Alors F est lipschitzienne (donc continue). En effet, pour tout \left(x,x'\right)\in\mathbb{R}^{2} :

    \begin{eqnarray*}\left|F\left(x\right)-F\left(x'\right)\right| & = & \left|\int_{0}^{1}f\left(t\right)\left[\varphi\left(xt\right)-\varphi\left(x't\right)\right]\thinspace dt\right|\\ & \leqslant & \int_{0}^{1}\left|f\left(t\right)\right|\thinspace\left|\varphi\left(xt\right)-\varphi\left(x't\right)\right|\thinspace dt \end{eqnarray*}

Or, par hypothèse, f est bornée (car continue sur un segment) et il existe k\geqslant0 tel que \left|\varphi\left(a\right)-\varphi\left(b\right)\right|\leqslant k\left|a-b\right| pour tout \left(a,b\right)\in\mathbb{R}^{2}. De ce fait :

    \begin{eqnarray*}\left|F\left(x\right)-F\left(x'\right)\right| & \leqslant & \left\Vert f\right\Vert_{\infty}\int_{0}^{1}\thinspace\left|\varphi\left(xt\right)-\varphi\left(x't\right)\right|\thinspace dt\\& \leqslant & k\left\Vert f\right\Vert_{\infty}\left|x-x'\right|\int_{0}^{1}t\thinspace dt\\& = & K\left|x-x'\right|\end{eqnarray*}

où l’on a posé :

    \[K=\frac{k}{2}\thinspace\left\Vert f\right\Vert _{\infty}\]

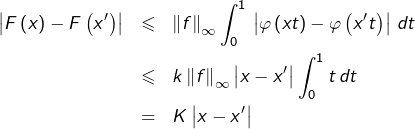
Théorème (de Picard)

Soit I est un intervalle fermé non trivial et soit f:I\to I une application contractante (c’est-à-dire k-lipschitzienne pour un certain k\in\left[0,1\right[).

Alors f possède un unique point fixe \lambda. De plus, pour tout s\in I, la suite définie par :

    \[\left\{\begin{matrix}x_0=s & \\\forall n\in\mathbb{N} & x_{n+1}=f(x_n)\end{matrix}\right.\]

converge vers \lambda.

On peut généraliser en remplaçant l’intervalle fermé I par un espace métrique complet. Une preuve de ce théorème est consultable dans cet article.

Partager cet article