Indications - Exercices sur l'uniforme continuité - 01

Pour le cas $\alpha>1,$ on pourra s’inspirer de ceci

Pour le cas $0<\alpha<1,$ on pourra s’inspirer de ceci

La réponse est non dans les deux cas.

Pour $L,$ le problème se situe en $0$ alors que pour $C,$ il se situe en $\pm\infty.$

Pour la somme, pas de souci (on peut se débrouiller facilement avec l’inégalité triangulaire).

Pour le produit, et sans hypothèses supplémentaires sur $f$ et $g,$ c’est faux : penser à $\mathbb{R}\rightarrow\mathbb{R},\thinspace x\mapsto x^{2}$ qui n’est pas UC mais qui est certainement le produit de deux applications UC !

Pour le produit de deux applications UC et bornées, on pourra s’inspirer de la preuve classique du fait que si deux suites réelles convergent, alors leur produit converge vers le produit des limites.

On se donne $\epsilon>0$ et l’on veut montrer qu’il existe $\alpha>0$ tel que, pour tout $\left(x,y\right)\in I^{2}$ :

$\left|x-y\right|\leqslant\alpha\Rightarrow\left|g\left(x\right)-g\left(y\right)\right|\leqslant\epsilon$

On peut écrire, artificiellement, pour tout $\left(x,y\right)\in I^{2}$ et pour tout $n\in\mathbb{N}$ :

$g\left(x\right)-g\left(y\right)=\left[g\left(x\right)-f_{n}\left(x\right)\right]+\left[f_{n}\left(x\right)-f_{n}\left(y\right)\right]+\left[f_{n}\left(y\right)-g\left(y\right)\right]$

Ensuite, c’est à vous 🙂

Se ramener à un segment et invoquer le théorème de Heine.

Attention : si $T$ est une période de $f,$ il est judicieux de considérer un segment de longueur $2T.$

Si l’on montre que $f$ est prolongeable en une application continue sur $\left[a,b\right],$ il en résultera que $f$ est bornée (pourquoi ?).

Penser à utiliser le critère de Cauchy.

Ca ressemble quand même beaucoup à une somme de Riemann, cette histoire !

Si besoin, consulter d’abord ceci.

Pour la question 1°, raisonner par l’absurde.

Pour la question 2°, essayer de construire $f:\mathbb{R}\rightarrow\mathbb{R}$ continue, positive et telle que :

$\forall n\in\mathbb{N}^{\star},\thinspace\int_{n-1}^{n}f\left(t\right)\thinspace dt=a_{n}$

où la série $\sum_{n\geqslant1}a_{n}$ converge.

Pour la question 3°, raisonner par l’absurde : si $f$ n’admet pas $0$ pour limite en $+\infty,$ alors il existe $\epsilon>0$ et une suite croissante $\left(x_{n}\right)_{n\geqslant0}$ telle que $\lim_{n\rightarrow\infty}x_{n}=+\infty$ et $\forall n\in\mathbb{N},\thinspace\left|f\left(x_{n}\right)\right|\geqslant2\epsilon.$ Et donc …

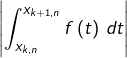Intuitivement, lorsque $n$ est assez grand, la fonction $f$ n’a « pas le temps » de changer de signe sur la plupart des segments $\left[x_{k,n},\thinspace x_{k+1,n}\right].$ L’intégrale $\left|\int_{x_{k,n}}^{x_{k+1,n}}f\left(t\right)\thinspace dt\right|$ est donc « le plus souvent » égale à ${\displaystyle \int_{x_{k,n}}^{x_{k+1,n}}\left|f\left(t\right)\right|\thinspace dt}.$

Ceci suggère de montrer (rigoureusement !) que :

$\lim_{n\rightarrow\infty}I_{n}=\int_{a}^{b}\left|f\left(t\right)\right|\thinspace dt$

Partager cet article