Indications - Exercices sur les suites numériques - 03

Indications pour démarrer les exercices sur les suites numériques (fiche 03).
Cliquer ici pour accéder aux énoncés.

Cette suite est définie par itération de $f:\left[0,1\right]\rightarrow\left[0,1\right],\thinspace t\mapsto\sqrt{1-t^{2}}.$ Calculer $f\circ f.$

La suite $S$ est croissante (d’évidence, $S_{n+1}-S_{n}\geqslant0$ pour tout $n\in\mathbb{N})$ . Il est n’est pas difficile de prouver qu’elle est aussi majorée.

Comme $x_{n}>0$ pour tout $n\in\mathbb{N}$ , on peut poser $y_{n}=\ln\left(x_{n}\right)$ .

Quelle relation de récurrence la suite $\left(y_{n}\right)_{n\in\mathbb{N}}$ vérifie-t-elle ?

Faire un dessin pour comprendre où se promène $x_{n}$ … L’étude des variations d’une fonction bien choisie permettra ensuite de prouver, pour chaque entier $n\geqslant2,$ l’existence et l’unicité d’une solution $x_{n}$ dans l’intervalle $\left]0,\pi\right[,$ pour cette équation.

Vous avez sans doute entendu parler de la conjecture de Collatz, aussi connue sous le nom de problème de Syracuse. L’énoncé de cette question lui ressemble furieusement …

Mais le problème de Syracuse reste à ce jour énigmatique, alors que cet exercice est parfaitement faisable !

Cette suite est construite en itérant à partir de s l’application :

$f:\mathbb{N}^\star\to\mathbb{N}^\star,n\mapsto\left\{\begin{matrix}\frac{n}{2} & \text{si }n\text{ est pair}\\n+5 & \text{sinon}\end{matrix}\right.$

Que se passe-t-il si $s=1$ ? Si $s=5$ ?

Prouver qu’en itérant à partir de n’importe quel entier $s\geqslant1$ , on finit par tomber sur 1 ou 5.

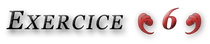
Plan de bataille proposé : trouver une suite $\left(T_{n}\right)$ assez simple, telle que $T_{n}$ soit du même signe que $S_{n}-S_{n+1},$ puis calculer le signe de $T_{n}-T_{n+1}.$

On pourra commencer par exprimer $S_{n}-S_{n+1}$ à l’aide de $\sum_{k=1}^{n}\frac{1}{\sqrt{k}}.$

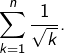
Les racines $n-$ èmes de l’unité sont les $e^{2ik\pi/n}$ pour $0\leqslant k\leqslant n-1.$ Par conséquent :

$D_{n}=\frac{1}{n-1}\sum_{k=1}^{n-1}\left|1-e^{2ik\pi/n}\right|$

Deux remarques :

Comment calcule-t-on 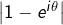$\left|1-e^{i\theta}\right|$ pour $\theta\in\left]0,2\pi\right[$ ?
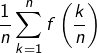Si $f:\left[0,1\right]\rightarrow\mathbb{R}$ est continue, quel scénario l’expression $\frac{1}{n}\sum_{k=1}^{n}f\left(\frac{k}{n}\right)$ évoque-t-elle ?

Etant donnée une suite réelle bornée $\left(x_k\right)_{k\geqslant0}$ , notons pour tout $n\in\mathbb{N}$ :

$X_{n}=\left\{ x_{k};\thinspace k\geqslant n\right\}$

Quelle relation existe-t-il entre les ensembles $X_{n+1}$ et $X_{n}$ ?
Que peut-on en déduire pour la suite $\left(\omega_{n}\right)_{n\in\mathbb{N}}$ ?

La convergence d’une suite $\left(z_{n}\right)_{n\geqslant0}$ et celle de la série $\sum_{n\geqslant0}\left(z_{n}-z_{n+1}\right)$ associée sont deux questions équivalentes.

Partager cet article