Indications pour démarrer les exercices sur les séries numériques (fiche 03).
Cliquer ici pour accéder aux énoncés.

icone-math-OS-Exos
exercice 1 facile

Il suffit de remarquer que la suite b est bornée !

exercice 2 facile

On peut faire apparaître une sommation télescopique en écrivant \frac{1}{n\left(n+p\right)} comme une différence de fractions.

Essayer d’encadrer u_{n} pour utiliser ensuite le principe de comparaison (à vous de voir, en tâtonnant, s’il est plus judicieux de majorer ou de minorer).

En notant S_{n} la n-ème somme partielle, on peut vérifier que la suite \left(S_{n^{2}}\right)_{n\geqslant1} est majorée.

Pour \alpha\neq1, comparer avec une série de Riemann et montrer que tout se passe « comme si le facteur \ln^{\beta}\left(n\right) était absent ». Pour \alpha=1, comparer avec une intégrale.

Pour la convergence, utiliser le résultat établi dans cet article concernant la nature des séries trigonométriques de la forme :

    \[\sum_{n\geqslant1}\frac{e^{in\theta}}{n^{s}}\]

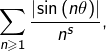Pour la divergence de la série {\displaystyle \sum_{n\geqslant1}\frac{\left|\sin\left(n\theta\right)\right|}{n^{s}}}, on peut minorer le terme général en exploitant le fait que :

    \[\forall t\in\left[0,1\right],\thinspace t\geqslant t^{2}\]

Utiliser la règle d’Abel (présentée dans cet article).

Pour le premier point, utiliser la formule de Taylor avec reste intégral pour la fonction exponentielle.

Pour le second, tâcher de majorer le reste R_{n} par la somme d’une série géométrique.

Pour le dernier point, appliquer le théorème des séries alternées en prenant soin d’en vérifier toutes les hypothèses.

exercice 9 difficile

En posant, pour tout n\in\mathbb{N} :

    \[A_{n}=\sum_{k=0}^{n}a_{k}\qquad B_{n}=\sum_{k=0}^{n}b_{k}\]

et

    \[X_{n}=\sum_{k=0}^{n}\left(\sum_{j=0}^{k}a_{j}b_{k-j}\right)\]

on peut montrer que :

    \[\lim_{n\rightarrow\infty}\left(X_{2n}-A_{n}B_{n}\right)=0\]

Il pourra être utile de dessiner le domaine de sommation W (partie finie de \mathbb{N}^{2}) pour lequel :

    \[X_{2n}-A_{n}B_{n}=\sum_{\left(i,j\right)\in W}a_{i}b_{j}\]

Partager cet article