Indications - Exercices sur les séries numériques - 01

Indications pour démarrer les exercices sur les séries numériques (fiche 01).
Cliquer ici pour accéder aux énoncés.

Il sera peut-être facile de traiter une question plus générale :

Etant données deux suites réelles $\left(a_{n}\right)_{n\geqslant1}$ et $\left(b_{n}\right)_{n\geqslant1}$ telles que les séries $\sum_{n\geqslant1}a_{n}^{2}$ et $\sum_{n\geqslant1}b_{n}^{2}$ convergent, on peut montrer que la série $\sum_{n\geqslant1}a_{n}b_{n}$ converge aussi.

Utiliser la règle des équivalents !

Rappel : si $\left(u_{n}\right)_{n\in\mathbb{N}}$ et $\left(v_{n}\right)_{n\in\mathbb{N}}$ sont deux suites de réels positifs telle que

$u_{n}\sim v_{n}\qquad\text{lorsque }n\rightarrow\infty$

alors les séries $\sum_{n\geqslant0}u_{n}$ et $\sum_{n\geqslant0}v_{n}$ sont de même nature.

L’hypothèse peut s’écrire :

$\forall n\in\mathbb{N},\thinspace0\leqslant b_{n}-a_{n}\leqslant c_{n}-a_{n}$

A partir de là, la réponse devrait être facile à trouver …

Si $r,s$ sont deux réels strictement positifs, alors :

$r^{\ln\left(s\right)}=e^{\ln\left(r\right)\ln\left(s\right)}$

mais cette dernière expression fait jouer à $r$ et $s$ des rôles symétriques ! Donc …

Commencer par exprimer la somme partielle 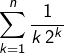$\sum_{k=1}^{n}\frac{1}{k\thinspace2^{k}}$ sous forme intégrale, grâce à l’égalité signalée dans l’énoncé.

Il faut pour commencer disposer d’une majoration du reste 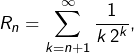${\displaystyle R_{n}=\sum_{k=n+1}^{\infty}\frac{1}{k\thinspace2^{k}}},$ ce que l’exercice précédent doit normalement apporter. Disons quelque chose du style :

$R_{n}\leqslant\alpha_{n}$

avec $\alpha_{n}$ connu explicitement et tel que $\lim_{n\rightarrow\infty}\alpha_{n}=0$ (à vous de voir …).

Après, on raisonne par condition suffisante : en notant 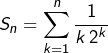$S_{n}=\sum_{k=1}^{n}\frac{1}{k\thinspace2^{k}}$ et ${\displaystyle \sigma=\lim_{n\rightarrow\infty}S_{n}},$ on cherche un entier $N$ tel que $\left|S_{N}-\sigma\right|\leqslant\epsilon$ où $\epsilon>0$ est donné.

Pour que cette condition soit remplie, il suffit que $\alpha_{n}\leqslant\epsilon.$

On peut adapter à ce contexte la preuve classique de la règle de d’Alembert : on distingue trois cas, selon que $\alpha>1,$ $\alpha<1$ ou $\alpha=1.$

Dans le premier cas, on se donne $\beta\in\left]1,\alpha\right[$ et l’on essaie de comparer $a_{n}$ et $\frac{1}{n^{\beta}}$ pour $n$ assez grand.

Déjà, il faut savoir que :

$\forall z\in\mathbb{C},\:e^{z}=\sum_{n=0}^{\infty}\frac{z^{n}}{n!}$

Ensuite, une bonne idée consiste à choisir convenablement $z.$

Commencer par vérifier que, pour tout $n\in\mathbb{N}^{\star},$ l’application $\left[0,1\right]\rightarrow\left[0,1\right],\thinspace t\mapsto\left(1-t^{n}\right)^{1/n}$ est une bijection décroissante et tracer son graphe.

Ce graphe présente une symétrie … laquelle et pourquoi ?

Tâcher d’interpréter le terme général de la série comme l’aire d’un domaine assez simple, puis décomposer ce domaine en sous-domaines dont l’aire est soit connue explicitement, soit facile majorer.

Partager cet article