Indications - Exercices sur la récurrence - 02

Indications pour démarrer les exercices sur le raisonnement par récurrence (fiche 02).
Cliquer ici pour accéder aux énoncés.

Regardez bien :

$f(x)=\frac{1}{1+x}\qquad\qquad f^2(x)=\frac{1}{1+\frac{1}{1+x}}=\frac{1+x}{1+2x}$

$f^3(x)=\frac{1}{1+\frac{1+x}{2+x}}=\frac{2+x}{3+x}\qquad\qquad f^4(x)=\frac{1}{1+\frac{2+x}{3+x}}=\frac{3+x}{5+x}$

Les coefficients 0, 1, 1, 2, 3, 5 … vous rappelent certainement quelque chose ! Eh oui : la suite de Fibonacci semble bien impliquée dans cette histoire !

Je vous suggère de calculer encore $f^5(x)$ pour passer d’une simple présomption à une quasi-conviction 🙂

En ensuite ? Récurrence, bien sûr…

Penser à la formule d’addition du sinus :

$\sin(a+b)=\sin(a)\cos(b)+\cos(a)\sin(b)$

pour transformer $\sin((n+1)x)$ .

Commencer par calculer $S_{n}$ pour $n=1$ , $n=2$ puis $n=3$ .

Ensuite, il va falloir se poser la question suivante :

Comment les parties non vides de $\mathbb{N}_{n+1}$ sont-elles obtenues à partir de celles de $\mathbb{N}_{n}$ ?

On peut calculer de deux façons la somme :

$\sum_{k=1}^{n}\left(\left(k+1\right)^{p+1}-k^{p+1}\right)$

et en déduire une formule de récurrence forte permettant le calcul de $S_{p}\left(n\right)$ . Vous pouvez aussi visionner cette vidéo, qui est précisément consacrée à cette question.

Développer séparément les expressions :

$\left(\sum_{i=1}^{n+1}a_{i}b_{i}\right)^{2}\qquad\textrm{et}\qquad\left(\sum_{i=1}^{n+1}\,a_{i}^{2}\right)\left(\sum_{i=1}^{n+1}\,b_{i}^{2}\right)$

en faisant intervenir :

$\left(\sum_{i=1}^{n}a_{i}b_{i}\right)^{2},\qquad\qquad\left(\sum_{i=1}^{n}\,a_{i}^{2}\right)\qquad\textrm{et}\qquad\left(\sum_{i=1}^{n}\,b_{i}^{2}\right)$

Le barycentre de $n+1$ nombres $x_1,\cdots,x_{n+1}$ affectés de poids $t_1,\cdots,t_{n+1}$ (avec $t_i\in[0,1]$ pour tout $i$ et $t_1+\cdots+t_{n+1}=1$ ) peut s’écrire comme un barycentre de deux nombres :

$\sum_{i=1}^{n+1}t_ix_i=T\sum_{i=1}^n\frac{t_i}{T}x_i+(1-T)x_{n+1}$

Je vous laisse le soin d’expliquer qui est ce nombre $T$ .

Pour l’hérédité, on considère une famille $\left(x_{1},\cdots,x_{n+1}\right)$ de vecteurs propres pour $u$ , associés à des valeurs propres toutes distinctes $\lambda_{1},\cdots,\lambda_{n+1}$ . On se donne une combinaison linéaire nulle des $x_{i}$ et on applique $u$ à chaque membre de cette égalité. En combinant ces deux égalités, on doit pouvoir éliminer le vecteur $x_{n+1}$ et obtenir une combinaison linéaire nulle de $x_{1},\cdots,x_{n}$ . On peut alors invoquer l’hypothèse de récurrence…

Vous pouvez, si vous le souhaitez, commencer à jeter un coup d’œil à cette vidéo, qui explique tout cela en détail.

Pour l’hérédité, on se donne $n+1$ vecteurs $x_{1},\cdots,x_{n+1}$ ainsi que $n+2$ vecteurs $y_{1},\cdots,y_{n+2}$ et l’on suppose que chaque $y_j$ est combinaison linéaire de $x_{1},\cdots,x_{n+1}$ .

Formaliser cela (en nommant les coefficients de toutes ces combinaisons linéaires, ce nécessitera une double indexation), puis distinguer deux cas, selon que :

les 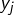$y_{j}$ sont tous combinaisons linéaires de $x_{1},\cdots,x_{n}$
ou pas !

Dans ce second cas, et quitte à renuméroter les vecteurs, on peut supposer que le $\left(n+1\right)-$ ème coefficient de la combinaison qui exprime $y_{1}$ à l’aide de $x_{1},\cdots,x_{n+1}$ est non nul, ce qui permet de diviser par ce scalaire…

Pour le 2°-c, développer le produit $\left(A-x_{i}\right)\left(x_{j}-A\right)$ .

Le reste de l’énoncé est suffisamment détaillé.

Partager cet article