

Pour ![]() c’est direct si vous connaissez une primitive de la fonction logarithme… et si vous ne connaissez pas, intégrez par parties… et si ceci n’aboutit pas, je vous suggère de jeter un œil au calcul de l’intégrale D, à la fin de cet article.
c’est direct si vous connaissez une primitive de la fonction logarithme… et si vous ne connaissez pas, intégrez par parties… et si ceci n’aboutit pas, je vous suggère de jeter un œil au calcul de l’intégrale D, à la fin de cet article.
Pour ![]() intégrer par parties.
intégrer par parties.

Deux intégrations par parties successives et le calcul de ![]() devrait aboutir !
devrait aboutir !
Il faut juste éviter que la seconde IPP ne neutralise la première…

Il faut commencer par « décomposer en éléments simples », c’est-à-dire trouver trois réels ![]() tels que, pour tout
tels que, pour tout ![]() :
:
![]()

Regarder attentivement la figure ci-dessous. Quelle inégalité exprime-t-elle ?
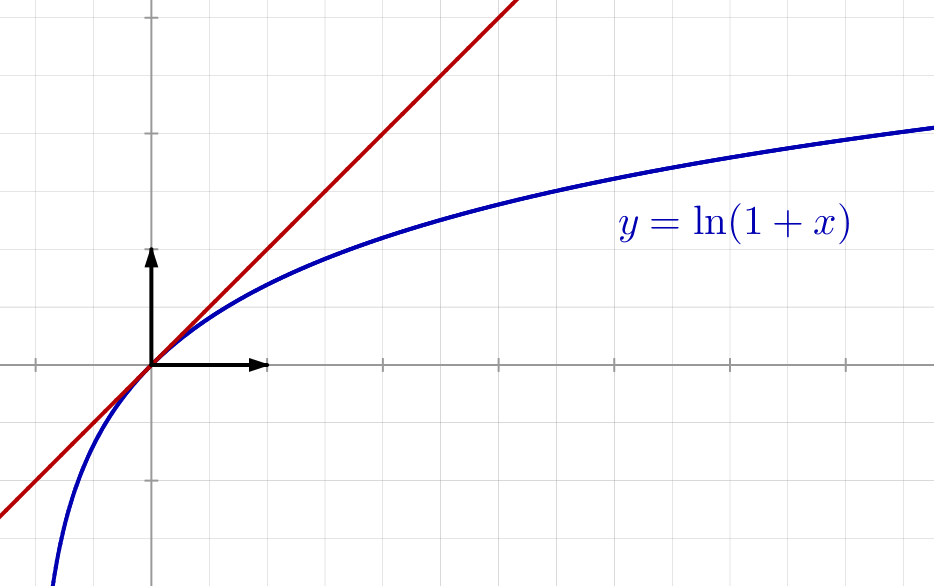

Le graphe fonction ![]() présente une symétrie par rapport à la droite d’équation
présente une symétrie par rapport à la droite d’équation ![]() Ceci suggère un changement de variable particulier, qui « exploite » cette symétrie.
Ceci suggère un changement de variable particulier, qui « exploite » cette symétrie.
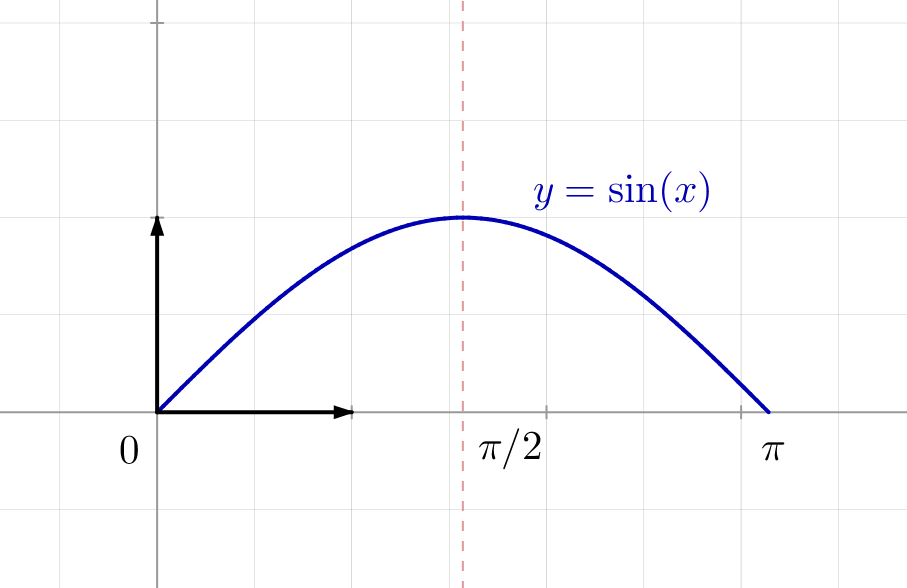

Comme ![]() est continue, il doit être intuitivement clair que, pour
est continue, il doit être intuitivement clair que, pour ![]() assez proche de
assez proche de ![]() l’intégrale de
l’intégrale de ![]() sur
sur ![]() est peu différente de l’intégrale, sur le même intervalle de la fonction constante
est peu différente de l’intégrale, sur le même intervalle de la fonction constante ![]() Cette remarque doit permettre de deviner la valeur de la limite demandée.
Cette remarque doit permettre de deviner la valeur de la limite demandée.
Bien entendu, il faut ensuite rendre tout cela rigoureux !

Même style d’indication que pour l’exercice précédent : lorsque ![]() est assez petit, il ne doit pas y avoir une grande différence entre les intégrales
est assez petit, il ne doit pas y avoir une grande différence entre les intégrales
![]()
Là encore , il s’agit d’une remarque intuitive qui doit vous mettre sur la voie d’une solution , mais une preuve rigoureuse doit rester l’objectif !
On sait que si ![]() est un intervalle (de longueur non nulle), si
est un intervalle (de longueur non nulle), si ![]() et si
et si ![]() est continue, alors l’application
est continue, alors l’application
![]()
En particulier, ![]() est de classe
est de classe ![]()
En utilisant ce résultat fondamental, on peut assez facilement montrer que toute solution de l’équation proposée est nécessairement de classe ![]() … ce qui donne le droit de dériver deux fois !
… ce qui donne le droit de dériver deux fois !

Si vous n’avez pas encore cherché l’exercice 4, il faut commencer par là !
Ensuite, une bonne chose à faire consiste à changer de variable et de poser ![]() dans l’intégrale qui définit
dans l’intégrale qui définit ![]()
