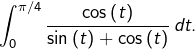icone-math-OS-Exos
exercice 1 facile
  • Pour A : l’intégrale d’une somme est égale à la somme des intégrales …
  • Pour B : la fonction intégrée est impaire !
  • Pour C : développer et appliquer l’indication donnée pour le A.
  • Pour D : quelle est la dérivée de t\mapsto\frac{1}{at+b} ?
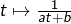  • Pour E : trouver 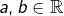a,b\in\mathbb{R} tels que 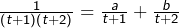\frac{1}{\left(t+1\right)\left(t+2\right)}=\frac{a}{t+1}+\frac{b}{t+2} pour tout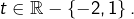 t\in\mathbb{R}-\left\{ -2,1\right\}.
  • Pour F : quelle est la dérivée de t\mapsto\frac{1}{\left(at+b\right)^{2}} ?
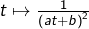  • Pour G : il y a un lien simple à trouver entre le numérateur et le dénominateur !
  • Pour H : Quelle est la dérivée de t\mapsto1+\frac{1}{t} ?
exercice 2 facile
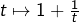  • Pour A : intégrer par parties.
  • Pour B : quelle est la dérivée de t\mapsto e^{t^{2}} ?
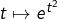  • Pour C : comment le numérateur et le dénominateur sont-ils liés ?
  • Pour D : il faut reconnaître le motif u^{n}u' …
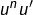  • Pour E : intégrer par parties.
  • Pour F : intégrer par parties (même astuce que pour le dernier exemple de cet article)
  • Pour G : intégrer par parties trois fois de suite.
  • Pour H : intégrer par parties en considérant que t^{3}e^{t^{2}}=t^{2}\:\left(t\thinspace e^{t^{2}}\right).
exercice 3 facile
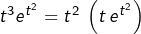  • Pour A : quelle est la dérivée de 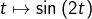t\mapsto\sin\left(2t\right) ? Et, plus généralement, de t\mapsto\sin\left(\lambda t\right) ?
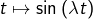  • Pour B : comment le numérateur et le dénominateur sont-ils liés ?
  • Pour C : intégrer par parties.
  • Pour D : intégrer par parties deux fois de suite.
  • Pour E : reconnaître le motif u'/\sqrt u.
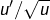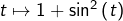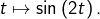  • Pour F : la dérivée de t\mapsto1+\sin^{2}\left(t\right) est t\mapsto\sin\left(2t\right). Reconnaître un motif familier !
  • Pour G : reconnaître le motif u'/u^2.
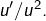
  • Pour H : calcul plus délicat. Considérer l’intégrale jumelle {\displaystyle \int_{0}^{\pi/4}\frac{\cos\left(t\right)}{\sin\left(t\right)+\cos\left(t\right)}\thinspace dt.}
Partager cet article