

Il suffit de voir que l’ensemble des diviseurs de ![]() (et à plus forte raison celui des diviseurs impairs) est inclus dans
(et à plus forte raison celui des diviseurs impairs) est inclus dans ![]() ce qui entraîne évidemment que :
ce qui entraîne évidemment que :
![]()
![]()
![Rendered by QuickLaTeX.com \[\sum_{n\geqslant1}\frac{1}{n^{2}}\qquad\sum_{n\geqslant1}\frac{1}{\sqrt{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bd59ab3106af339dde359c1bed30fc87_l3.png)

Fixons ![]() tel que
tel que ![]() Pour
Pour ![]() assez grand :
assez grand :
![]()
![]()
Exemple d’utilisation
Si l’on pose, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[a_{n}=\left(1-\frac{1}{n}\right)^{n^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8179fd1ebece19488ef785f6e514b92a_l3.png)
![]()
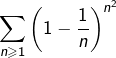 est donc convergente.
est donc convergente.
Remarque
Cette méthode (qui donne une condition suffisante de convergence pour une série à termes positifs) est connue sous le nom de règle de Cauchy.

La propriété des croissances comparées (entre une exponentielle et une puissance) nous dit que, peu importe la valeur du réel ![]() :
:
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}\ln\left(n^{\mu}e^{-\sqrt{n}}\right) & = & \mu\ln\left(n\right)-\sqrt{n}\\& = & 2\mu\ln\left(\sqrt{n}\right)-\sqrt{n}\\& = & \sqrt{n}\left[2\mu\thinspace\frac{\ln\left(\sqrt{n}\right)}{\sqrt{n}}-1\right]\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-e76a0935e7eb7ae31ba45a113f6e81e6_l3.png)
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{n\geqslant N\Rightarrow0<n^{\lambda}e^{-\sqrt{n}}\leqslant\frac{1}{n^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-be8da8efec3187537564dd45138236ce_l3.png)

Pour tout ![]() et pour tout
et pour tout ![]() vu que
vu que ![]() :
:
![]()
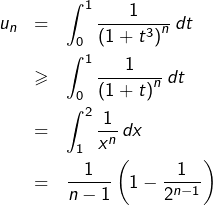
![]()
Remarque
Dans ce qui précède, l’exposant 3 ne joue aucun rôle particulier et peut être remplacé par n’importe quel réel ![]() fixé.
fixé.

On observe que :
![]()
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}\frac{1}{n}\sum_{k=1}^{n}k^{1/k}=1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3006fc52898e790977b89bb8dfdc7e1b_l3.png)
![]()

Observons pour commencer que, si l’on pose :
![Rendered by QuickLaTeX.com \[x_{n}=\left[\cos\left(\frac{1}{n}\right)\right]^{n^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e512f4d1b4dc3f65e2353b19b88317f6_l3.png)
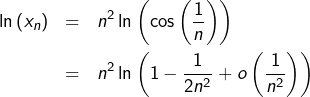
![]()
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}x_{n}=\frac{1}{\sqrt{e}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d079211b2473a5fe8b7ef336c51c494b_l3.png)
L’idée est de reprendre le développement asymptotique précédent, mais avec une précision accrue. On part de :
![]()
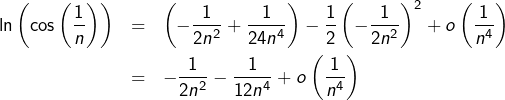
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{q_{n}\sim\frac{1}{12\sqrt{e}n^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bd251de02409e2ee1005e1b67ec06de8_l3.png)

Il est connu que, pour tout ![]() :
:
![]()
 par hypothèse
par hypothèse- si
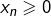 pour un certain
pour un certain 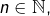 alors
alors 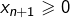 car
car 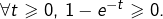
La suite ![]() converge donc vers un réel
converge donc vers un réel ![]() En passant à la limite dans l’égalité
En passant à la limite dans l’égalité ![]() et compte tenu de la continuité de la fonction exponentielle :
et compte tenu de la continuité de la fonction exponentielle : ![]()
Or, une étude (non détaillée) des variations de ![]() montre que cette application possède 0 comme unique point fixe. Ainsi
montre que cette application possède 0 comme unique point fixe. Ainsi ![]()
On peut maintenant utiliser le développement limité au second ordre :
![]()
![]()
![]()
Donc, étant donné ![]() :
:
![Rendered by QuickLaTeX.com \begin{eqnarray*}x_{n+1}^{\lambda}-x_{n}^{\lambda} & = & \left(x_{n}-\frac{x_{n}^{2}}{2}+o\left(x_{n}^{2}\right)\right)^{\lambda}-x_{n}^{\lambda}\\& = & x_{n}^{\lambda}\left[\left(1-\frac{x_{n}}{2}+o\left(x_{n}\right)\right)^{\lambda}-1\right]\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-3fdbc42b7ebc5c1cbb4f7a2ecc2f6e43_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}\left(\frac{1}{x_{n+1}}-\frac{1}{x_{n}}\right)=\frac{1}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-68508e91ac6cfcf4a20c0f999489a832_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}\frac{1}{n}\sum_{k=0}^{n-1}\left(\frac{1}{x_{k+1}}-\frac{1}{x_{k}}\right)=\frac{1}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e559c3e9d3e3aef118a957be22643d63_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{x_{n}\sim\frac{2}{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-45443bf9051dff4fd9b551560418058c_l3.png)

En posant ![]() et
et 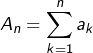 si
si ![]() on constate que, pour tout
on constate que, pour tout ![]() :
:
![]()
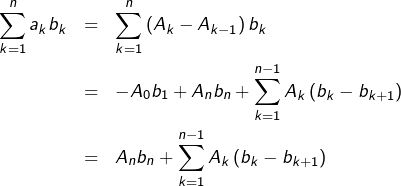
La suite ![]() est aussi convergente (c’est par hypothèse la suite des sommes partielles d’une série convergente). Notons
est aussi convergente (c’est par hypothèse la suite des sommes partielles d’une série convergente). Notons ![]() sa limite et notons
sa limite et notons ![]() un majorant de
un majorant de ![]() Alors, d’une part :
Alors, d’une part :
![]()
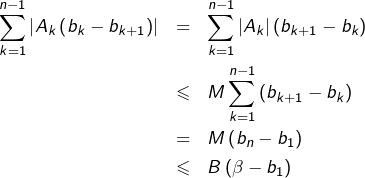
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}\sum_{k=1}^{n}a_{k}b_{k}=\sigma\beta+S\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4f5821c31e643d1ba638cf356463d39b_l3.png)

Une possibilité consiste à poser, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{t_{n}=\frac{1}{n^{1/3}}}\qquad\text{et}\qquad\boxed{z_{n}=e^{2in\pi/3}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bdb3c561b541888b3ffa055e7357b3fa_l3.png)
Quant aux sommes partielles 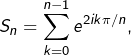 on reconnaît qu’il s’agit de sommes géométriques (de raison
on reconnaît qu’il s’agit de sommes géométriques (de raison ![]() et on les calcule donc comme suit :
et on les calcule donc comme suit :
![]()
![]()
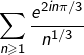 converge.
converge.
Cependant, la série 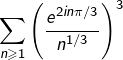 diverge, puisque son terme général n’est autre que
diverge, puisque son terme général n’est autre que ![]()
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
