

Calcul détaillé de 8 intégrales (de polynômes et de fractions rationnelles de petits degrés).
Calcul de ![]()
![Rendered by QuickLaTeX.com \[A=\left[\frac{t^{4}}{4}-t^{2}\right]_{0}^{1}=\frac{1}{4}-1=\boxed{-\frac{3}{4}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-67ccc0e6d798f8fe927f3c8d29c95313_l3.png)
Calcul de ![]()
La propriété utilisée est la suivante :
Proposition
Si ![]() est une fonction continue et impaire, alors
est une fonction continue et impaire, alors ![]()
On peut prouver ceci en changeant de variable (poser ![]()
Et si vous ne connaissez pas l’intégration par changement de variable, pas de souci …
Notons ![]() la primitive de
la primitive de ![]() qui s’annule en 0 et posons, pour tout
qui s’annule en 0 et posons, pour tout ![]() :
:
![]()
![]()
Et donc ![]() est constante. Mais comme
est constante. Mais comme ![]() alors
alors ![]() est nulle.
est nulle.
Ceci montre que ![]() est paire et donc que :
est paire et donc que :
![]()
Calcul de ![]()
Le plus simple est de développer. On trouve, pour tout ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[C=\left[\frac{t^{7}}{7}+\frac{3t^{5}}{5}+t^{3}+t\right]_{0}^{1}=\frac{1}{7}+\frac{3}{5}+1+1=\boxed{\frac{96}{35}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b34e25d76d4bf0c6f0672c989b43cce1_l3.png)
Calcul de ![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}D & = & \left[2\ln\left(t+3\right)-\frac{1}{2}\ln\left(2t+1\right)\right]_{0}^{1}\\& = & 2\ln\left(4\right)-\frac{1}{2}\ln\left(3\right)-\left(2\ln\left(3\right)-\frac{1}{2}\ln\left(1\right)\right)\\& = & \boxed{4\ln\left(2\right)-\frac{5}{2}\ln\left(3\right)}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-1d4099eaa7199b80637d8e15d00ba157_l3.png)
Compte tenu des propriétés de la fonction logarithme, on peut encore écrire : ![]()
Calcul de ![]()
On observe que, pour tout ![]() :
:
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{E=\ln\left(\frac{4}{3}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2a7876b44390d9a6d435b5e100696478_l3.png)
Calcul de 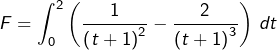
![Rendered by QuickLaTeX.com \[F=\left[-\frac{1}{t+1}+\frac{1}{\left(t+1\right)^{2}}\right]_{0}^{2}=-\frac{1}{3}+\frac{1}{9}-\left(-1+1\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-08b762e24b7a53503ae37e66ca98c006_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{F=-\frac{2}{9}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bbede042b6dc1462c293c768d04b9d79_l3.png)
Calcul de ![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{G=\frac{1}{2}\ln\left(\frac{5}{2}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2a44a9fec77ed82eef642637ea386d2e_l3.png)
Calcul de ![]()
On développe :
![Rendered by QuickLaTeX.com \begin{eqnarray*}H & = & \int_{1}^{2}\left(\frac{1}{t^{2}}+\frac{2}{t^{3}}+\frac{1}{t^{4}}\right)\thinspace dt\\& = & \left[-\frac{1}{t}-\frac{1}{t^{2}}-\frac{1}{3t^{3}}\right]_{1}^{2}\\& = & \left(-\frac{1}{2}-\frac{1}{4}-\frac{1}{24}\right)-\left(-1-1-\frac{1}{3}\right) \end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-890eee33bebf36a39f85d6291b32d821_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{H=\frac{37}{24}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-59317bc57391c2d99975b9363ba1b832_l3.png)
Calcul détaillé de 8 intégrales (de fonctions composées d’exponentielles (ou de logarithmes) et de polynômes).
Calcul de ![]()
On intègre par parties en posant :
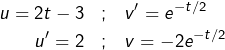
On obtient :
![Rendered by QuickLaTeX.com \begin{eqnarray*}A & = & \left[-2\left(2t-3\right)e^{-t/2}\right]_{0}^{1}+\int_{0}^{1}4\thinspace e^{-t/2}\thinspace dt\\& = & 2\thinspace e^{-1/2}-6+4\left[-2e^{-t/2}\right]_{0}^{1}\\& = & 2\thinspace e^{-1/2}-6+4\left(-2\thinspace e^{-1/2}+2\right)\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-0a62b343daabb7927467d7e39fd60940_l3.png)
![]()
Calcul de ![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{B=\frac{e-1}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2fff6073020ed45fc97da832ac21c00e_l3.png)
Calcul de ![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{C=\ln\left(\frac{e+1}{2}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b0b39fbcc9a6f529037df41b861bc78b_l3.png)
Calcul de ![]()
![Rendered by QuickLaTeX.com \[D=\left[\frac{1}{4}\left(1+e^{t}\right)^{4}\right]_{-1}^{1}=\frac{1}{4}\left(\left(1+e\right)^{4}-\left(1+\frac{1}{e}\right)^{4}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4ba63352d420cad5b78af31121fa07d4_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{D=\frac{\left(1+e\right)^{4}}{4}\left(1-\frac{1}{e^{4}}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2ffa25278e746378a3c8ac591fa92f3b_l3.png)
Calcul de ![]()
On intègre par parties en posant :
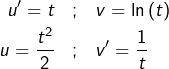
![Rendered by QuickLaTeX.com \begin{eqnarray*}E & = & \left[\frac{t^{2}}{2}\ln\left(t\right)\right]_{1}^{e}-\int_{1}^{e}\frac{t}{2}\thinspace dt\\& = & \frac{e^{2}}{2}-\left[\frac{t^{2}}{4}\right]_{1}^{e}\\& = & \boxed{\frac{e^{2}+1}{4}}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-d5f839fd5f0fd571114709d752242ec8_l3.png)
Calcul de ![]()
On intègre par parties en posant :
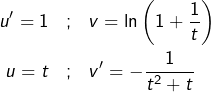
On obtient :
![Rendered by QuickLaTeX.com \begin{eqnarray*}F & = & \left[t\ln\left(1+\frac{1}{t}\right)\right]_{1}^{2}+\int_{1}^{2}\frac{1}{t+1}\thinspace dt\\& = & 2\ln\left(\frac{3}{2}\right)-\ln\left(2\right)+\left[\ln\left(t+1\right)\right]_{1}^{2}\\& = & 2\ln\left(\frac{3}{2}\right)-\ln\left(2\right)+\ln\left(3\right)-\ln\left(2\right)\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-99547c6b52ca845a34c8eea5ed4b0c9e_l3.png)
![]()
Calcul de ![]()
On intègre trois fois (!) par parties.
➡ Première IPP :
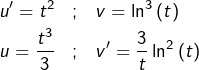
qui donne :
![]()
➡ Seconde IPP (pour ![]() :
:
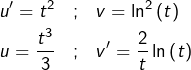
![]()
➡ Troisième IPP (pour ![]() :
:
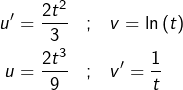
![Rendered by QuickLaTeX.com \begin{eqnarray*}G_{2} & = & \left[\frac{2t^{3}}{9}\ln\left(t\right)\right]_{1}^{e}-\int_{1}^{e}\frac{2t^{2}}{9}\thinspace dt\\& = & \frac{2e^{3}}{9}-\left[\frac{2t^{3}}{27}\right]_{1}^{e}\\& = & \frac{2e^{3}}{9}-\left(\frac{2e^{3}}{27}-\frac{2}{27}\right)\\& = & \frac{4e^{3}+2}{27}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-f69514fc4852fd0327cbfb1e28932f6c_l3.png)
Maintenant, on doit coller les morceaux …
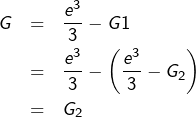
![Rendered by QuickLaTeX.com \[\boxed{G=\frac{4e^{3}+2}{27}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e782fc8ca14510a75d32eaae757730c6_l3.png)
Calcul de ![]()
On intègre par parties en posant :
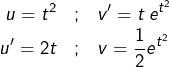
ce qui donne :
![Rendered by QuickLaTeX.com \begin{eqnarray*}H & = & \left[\frac{t^{2}}{2}e^{t^{2}}\right]_{0}^{1}-\int_{0}^{1}t\thinspace e^{t^{2}}\thinspace dt\\& = & \frac{e}{2}-\left[\frac{1}{2}e^{t^{2}}\right]_{0}^{1}\\& = & \boxed{\frac{1}{2}}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-4eda5b30044c55c4ee359354cca01bb9_l3.png)

Calcul détaillé de 8 intégrales trigonométriques.
Calcul de ![]()
![Rendered by QuickLaTeX.com \[A=\left[\frac{1}{2}\sin\left(2t\right)\right]_{0}^{\pi/6}=\frac{1}{2}\sin\left(\frac{\pi}{3}\right)=\boxed{\frac{\sqrt{3}}{4}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f77075b9f393e5bbd0d387ea0e882f0c_l3.png)
Calcul de 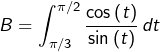
![Rendered by QuickLaTeX.com \begin{eqnarray*}B & = & \left[\ln\left(\sin\left(t\right)\right)\right]_{\pi/3}^{\pi/2}\\& = & -\ln\left(\sin\left(\frac{\pi}{3}\right)\right)\\& = & -\ln\left(\frac{\sqrt{3}}{2}\right)\\ & = & \boxed{\ln\left(2\right)-\frac{1}{2}\ln\left(3\right)}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-42697d7680cdcdf1ffb8866b2b960c44_l3.png)
ou, ce qui revient au même :
Calcul de ![]()
On intègre par parties en posant :
![]()
ce qui donne :
![Rendered by QuickLaTeX.com \begin{eqnarray*}C & = & \left[t\sin\left(t\right)\right]_{0}^{\pi}-\int_{0}^{\pi}\sin\left(t\right)\thinspace dt\\& = & \boxed{-2}\end{eqnarray}](https://math-os.com/wp-content/ql-cache/quicklatex.com-13dd37d05060e76889ccde3df70ca146_l3.png)
Calcul de ![]()
On intègre deux fois par parties, en dérivant à chaque fois le facteur polynomial (ce qui a pour effet de le faire disparaître).
➡ Première IPP :
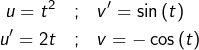
donc :
![]()
➡ Seconde IPP (pour ![]() :
:
![]()
ce qui donne :
![Rendered by QuickLaTeX.com \begin{eqnarray*}D_{1} & = & \left[2t\sin\left(t\right)\right]_{0}^{\pi}-\int_{0}^{\pi}2\sin\left(t\right)\thinspace dt\\& = & -\left[-2\cos\left(t\right)\right]_{0}^{\pi}\\& = & -4\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-5ae4e08d84e03c4e7b594a464b31272a_l3.png)
![]()
Calcul de 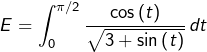
![Rendered by QuickLaTeX.com \[E=2\int_{0}^{\pi/2}\frac{u'\left(t\right)}{2\sqrt{u\left(t\right)}}\thinspace dt\qquad\text{avec }u\left(t\right)=3+\sin\left(t\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5ca73e6fc92f9f19522b00de07ec842f_l3.png)
![]()
Calcul de ![]()
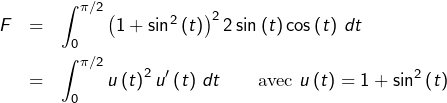
Par conséquent :
![Rendered by QuickLaTeX.com \[F=\left[\frac{1}{3}u\left(t\right)^{3}\right]_{0}^{\pi/2}=\frac{1}{3}\left(2^{3}-1\right)=\boxed{\frac{7}{3}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-def90b1bc4502f4f72690d087b63d5f2_l3.png)
Calcul de 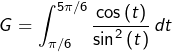
![Rendered by QuickLaTeX.com \[G=\int_{\pi/6}^{5\pi/6}\frac{u'\left(t\right)}{u\left(t\right)^{2}}\thinspace dt\qquad\text{avec }u\left(t\right)=\sin\left(t\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-39d17b751d8b8610fd62d655db83e534_l3.png)
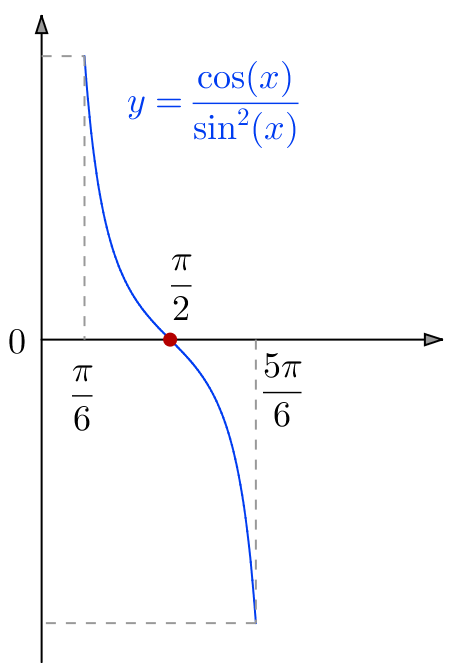
![Rendered by QuickLaTeX.com \[G=\left[-\frac{1}{\sin\left(t\right)}\right]_{\pi/6}^{5\pi/6}\qquad\text{càd : }\boxed{G=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-705872628c5fb137f1fd11e2952ec042_l3.png)
Ce résultat pouvait être obtenu sans calcul. En effet, si l’on pose ![]() et
et
![]()
![]()
La nullité de l’intégrale en résulte.
Calcul de ![]()
Si l’on pose :
![]()
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}K-H & = & \int_{0}^{\pi/4}\frac{\cos\left(t\right)-\sin\left(t\right)}{\sin\left(t\right)+\cos\left(t\right)}\thinspace dt\\& = & \left[\ln\left(\sin\left(t\right)+\cos\left(t\right)\right)\right]_{0}^{\pi/4}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-0c6f478ae2177711d4f0cff1a8ba2ca1_l3.png)
![]()
Il en résulte, par différence membre à membre de ![]() et
et ![]() , que :
, que :
![Rendered by QuickLaTeX.com \[\boxed{H=\frac{\pi}{8}-\frac{1}{4}\ln\left(2\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-79e6ba5b24d788a71de161d7f66d7d54_l3.png)
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
