(![]() )
) ![]()
Solution 1
Méthode 1
![]()
Méthode 2
![]()
![]()
![]()
![]()
Solution 2
![]()
(![]() )
) ![]()
- Si
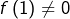 (et donc
(et donc 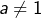 ), alors en choisissant
), alors en choisissant 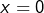 dans
dans 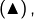 on obtient
on obtient 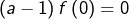 et donc
et donc 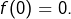 On peut alors prendre
On peut alors prendre 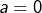 et la relation
et la relation  devient :
devient :
La fonction![Rendered by QuickLaTeX.com \[\forall x\in\mathbb{R},\ f(\left|x\right|)=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-15f575b2a7f3fef9c80b7c4077f20280_l3.png)
 est donc nulle sur
est donc nulle sur 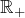 , d’où contradiction puisqu’on a supposé que
, d’où contradiction puisqu’on a supposé que 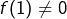 .
. - Si
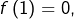 alors on prend
alors on prend 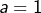 et la relation
et la relation  devient :
devient :
La fonction![Rendered by QuickLaTeX.com \[\forall x\in\mathbb{R},\quad f(\left|x\right|)=f(x)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-243a8d417ce9817a7841572055fcc9fe_l3.png)
 est donc paire. La relation
est donc paire. La relation 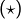 prend la forme :
prend la forme :
En choisissant![Rendered by QuickLaTeX.com \[\forall(x,y)\in\mathbb{R}^{2},\thinspace f(x+f(y))=xf(y)+yf(x)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-833cafa33eefcbb444a4d539bcd1f159_l3.png)
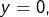 il vient :
il vient : (
On choisit alors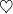 )
) ![Rendered by QuickLaTeX.com \[\forall x\in\mathbb{R},\thinspace f(x+f(0))=xf(0)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6e13536eb53adbc44cb4b62d30f672b8_l3.png)
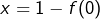 , ce qui donne
, ce qui donne 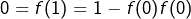 soit
soit 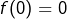 ou
ou 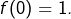 Dans le cas où
Dans le cas où 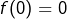 , la relation
, la relation  devient :
devient : ![Rendered by QuickLaTeX.com \[\forall x\in\mathbb{R},\thinspace f(x)=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-312c7b3363576bc9f04546b21f8cded6_l3.png)
 est donc l’application nulle. Et si
est donc l’application nulle. Et si 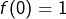 , la relation
, la relation  devient :
devient :
Alors![Rendered by QuickLaTeX.com \[\forall x\in\mathbb{R},\thinspace f(x+1)=x\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-18bb53c1755ee2ab03ce0db8e7f06008_l3.png)
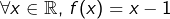 , mais c’est absurde puisque
, mais c’est absurde puisque  est paire.
est paire.

