Solution pour le challenge 85
Considérons une bijection continue ![]() admettant
admettant ![]() pour limite en
pour limite en ![]() et montrons que sa réciproque possède la même propriété.
et montrons que sa réciproque possède la même propriété.
Comme ![]() est continue (sur un intervalle) et injective, elle est strictement monotone. Et vue sa limite en
est continue (sur un intervalle) et injective, elle est strictement monotone. Et vue sa limite en ![]() elle est croissante. Il s’ensuit que pour tout
elle est croissante. Il s’ensuit que pour tout ![]() :
:
![]()
![]()
Maintenant, montrons que cette conclusion n’est pas maintenue sans l’hypothèse de continuité.
Commençons par construire une bijection ![]() vérifiant :
vérifiant :
![]()
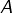 l’ensemble des entiers strictement négatifs
l’ensemble des entiers strictement négatifs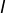 l’ensemble des entiers naturels impairs
l’ensemble des entiers naturels impairs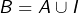
Soit ![]() une bijection (
une bijection (![]() et
et ![]() sont équipotents en tant que parties infinies de
sont équipotents en tant que parties infinies de ![]() Considérons l’application :
Considérons l’application :
![Rendered by QuickLaTeX.com \[g:\mathbb{Z}\rightarrow\mathbb{Z},\thinspace n\mapsto\left\{ \begin{array}{cc}2n & \text{si }n\in\mathbb{N}\\\\\varphi\left(n\right) & \text{si }n\in A\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8151b52a4bbcf81879b9131ed148d13a_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\boxed{f:\mathbb{R\rightarrow\mathbb{R}},\thinspace x\mapsto\left\{ \begin{array}{cc}g\left(x\right) & \text{si }x\in\mathbb{Z}\\\\x & \text{sinon}\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f3febdc23a991108c0cc75a8d004638e_l3.png)
![]()
![]()
Pour consulter l’énoncé, c’est ici

