Solution pour le challenge 84
Soit ![]() et soit
et soit ![]()
Manifestement, ![]() n’est pas une puissance parfaite. Désormais, on suppose :
n’est pas une puissance parfaite. Désormais, on suppose : ![]() L’égalité
L’égalité ![]() montre que
montre que ![]() est strictement compris entre deux carrés parfaits consécutifs, ce qui prouve que
est strictement compris entre deux carrés parfaits consécutifs, ce qui prouve que ![]() n’est pas un carré parfait (et donc pas non plus une puissance parfaite d’exposant pair).
n’est pas un carré parfait (et donc pas non plus une puissance parfaite d’exposant pair).
Supposons maintenant que ![]() avec des entiers
avec des entiers ![]() et
et ![]() tels que :
tels que : ![]()
![]() et
et ![]() impair.
impair.
L’entier ![]() est aussi impair, puisque
est aussi impair, puisque ![]() est impair. D’après une identité remarquable bien connue :
est impair. D’après une identité remarquable bien connue :
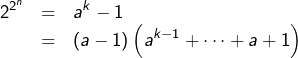
Ceci est absurde car ![]() ne possède aucun diviseur impair strictement supérieur à 1.
ne possède aucun diviseur impair strictement supérieur à 1.
Cette contradiction montre qu’aucun nombre de Fermat n’est une puissance parfaite.
Pour consulter l’énoncé, c’est ici


Merci!
La preuve semble aussi fonctionner pour les nombres 2^{2n}+1. Idem pour les 2^{2n+1}+1, du moins sur la partie k impair. Mais pour k pair ? Si on calcule quelques cas, ça « a l’air » de continuer à être vrai. Mais on est sur une forme 2.2^{2n}+1, soit 2A²+1. Qui peut être un carré parfait, comme par exemple 2.12²+1=17². Y-aurait-il une raison pour laquelle ça continue à être vrai avec A=2^{2n}, ou est-ce mon « exploration calculatoire » qui ne va pas assez loin pour trouver des contre-exemples?
Les entiers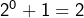 et
et 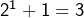 ne sont pas des puissances parfaites. L’entier
ne sont pas des puissances parfaites. L’entier 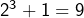 est un carré parfait. Supposons désormais
est un carré parfait. Supposons désormais 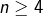 et
et 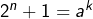 avec
avec 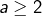 et
et 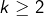 . Si
. Si 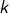 est pair, alors
est pair, alors 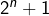 est un carré parfait :
est un carré parfait : 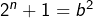 , donc
, donc 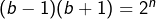 , ce qui impose que
, ce qui impose que  et
et 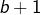 soient des puissances de
soient des puissances de 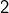 . La seule issue est
. La seule issue est 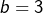 d’où
d’où 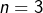 , qu’on a exclu plus haut. Supposons maintenant
, qu’on a exclu plus haut. Supposons maintenant 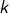 impair. On a :
impair. On a : 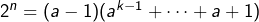 , donc en particulier
, donc en particulier  est une puissance de
est une puissance de 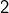 , strictement supérieure à
, strictement supérieure à 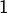 . Mais
. Mais  et
et 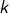 étant impairs,
étant impairs,  est aussi impair : contradiction.
est aussi impair : contradiction.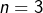 , l’entier
, l’entier 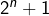 n’est jamais une puissance parfaite.
n’est jamais une puissance parfaite.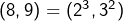 . Mais pour prouver ce résultat, c’est une autre paire de manches …
. Mais pour prouver ce résultat, c’est une autre paire de manches …
Moralité : hormis le cas
Tout ceci constitue un cas très particulier de la conjecture de Catalan, démontrée en 2002 par Preda Mihailescu : il n’existe aucun couple d’entier naturels consécutifs qui soient tous deux des puissances parfaites, à l’exception de
Merci beaucoup. J’espère qu’en mettant des , mes formules latex seront remplacées.
On peut donc en déduire n’est pas non plus une puissance?
n’est pas non plus une puissance?
Pour cas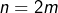 :
:
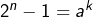 implique
implique 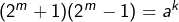 , donc
, donc 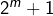 et
et 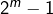 des puissances. D’après la démonstration précédente, le premier facteur donne l’unique solution m=3. Mais
des puissances. D’après la démonstration précédente, le premier facteur donne l’unique solution m=3. Mais 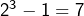 . Il n’y a donc aucune solution.
. Il n’y a donc aucune solution.
Pour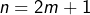 :
: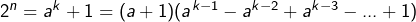 .
.  est impair, donc le raisonnement de la démonstration précédente semble s’appliquer aussi
est impair, donc le raisonnement de la démonstration précédente semble s’appliquer aussi
Si k impair, alors
Si k est pair, là je suis perdu … qu’en pensez-vous ?
J’ai ceci: si k est pair,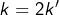 , alors
, alors 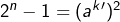 donne -1\equiv 1 ~ (mod 4)
donne -1\equiv 1 ~ (mod 4)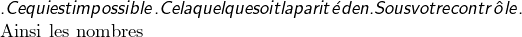 2^n\pm 2^m=2^{n-m}(2^{m}\pm 1), ~ m<n
2^n\pm 2^m=2^{n-m}(2^{m}\pm 1), ~ m<n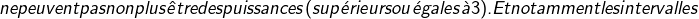 [[2^n-2;2^n+2]]
[[2^n-2;2^n+2]]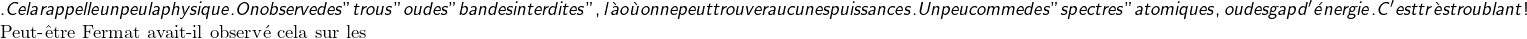 2^n\pm1
2^n\pm1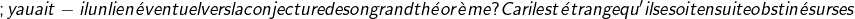 F_n=2^{2^n}+1$, avec notamment sa fausse conjecture sur la primalité.
F_n=2^{2^n}+1$, avec notamment sa fausse conjecture sur la primalité.
Il a manqué un « dollar ». Désolé. Je reposte.
J’ai ceci: si k est pair,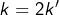 , alors
, alors 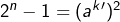 donne
donne 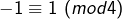 . Ce qui est impossible. Cela quelque soit la parité de n.
. Ce qui est impossible. Cela quelque soit la parité de n.
Sous votre contrôle.
Ainsi les nombres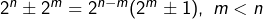 ne peuvent pas non plus être des puissances (supérieurs ou égales à 3). Et notamment les intervalles
ne peuvent pas non plus être des puissances (supérieurs ou égales à 3). Et notamment les intervalles ![Rendered by QuickLaTeX.com [[2^n-2;2^n+2]]](https://math-os.com/wp-content/ql-cache/quicklatex.com-59aec59351514e55009e128d484b3b0e_l3.png) . Cela rappelle un peu la physique. On observe des "trous" ou des "bandes interdites", là où on ne peut trouver aucunes puissances. Un peu comme des "spectres" atomiques, ou des gap d'énergie. C'est très troublant!
. Cela rappelle un peu la physique. On observe des "trous" ou des "bandes interdites", là où on ne peut trouver aucunes puissances. Un peu comme des "spectres" atomiques, ou des gap d'énergie. C'est très troublant!
Peut-être Fermat avait-il observé cela sur les ; y auait-il un lien éventuel vers la conjecture de son grand théorème? Car il est étrange qu'il se soit ensuite obstiné sur ses
; y auait-il un lien éventuel vers la conjecture de son grand théorème? Car il est étrange qu'il se soit ensuite obstiné sur ses 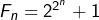 , avec notamment sa fausse conjecture sur la primalité.
, avec notamment sa fausse conjecture sur la primalité.
Oui, bien sûr. Si l’on note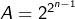 , alors l’égalité
, alors l’égalité 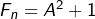 montre que
montre que 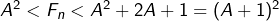 . Ainsi
. Ainsi 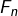 est strictement compris entre deux carrés parfaits consécutifs. Ce n’est donc pas un carré parfait. Peut-être qu’un exemple numérique permettra de mieux voir ce qui se passe : les entiers
est strictement compris entre deux carrés parfaits consécutifs. Ce n’est donc pas un carré parfait. Peut-être qu’un exemple numérique permettra de mieux voir ce qui se passe : les entiers 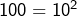 et
et 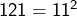 sont des carrés parfaits consécutifs. Si un entier
sont des carrés parfaits consécutifs. Si un entier 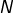 est compris entre
est compris entre 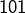 et
et 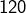 (inclusivement), alors
(inclusivement), alors 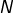 n’est certainement pas un carré parfait.
n’est certainement pas un carré parfait.
Bonjour. Merci beaucoup pour ce problème (et la solution)
Pourriez-vous détailler la partie « k pair »: F_n compris entre 2 carrés parfait consécutifs, donc pas un carré parfait ?