Solution pour le challenge 62
La réponse est non. Pour le voir, considérons la suite définie par :
![]()
![Rendered by QuickLaTeX.com \[y_{n}=\frac{1}{n+1}\sum_{k=0}^{n}\left(-1\right)^{k}\sqrt{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-228feb80375bc03c34e535910337af9b_l3.png)
Alors :
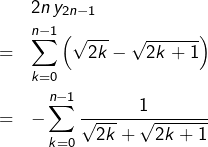
![]()
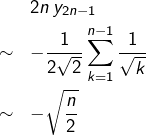
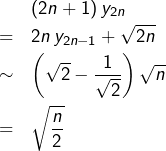
Bref :
![Rendered by QuickLaTeX.com \[\boxed{y_{n}\sim\frac{\left(-1\right)^{n}}{2\sqrt{n}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-646cc2ef8e5137e37cec1b04a54f7451_l3.png)
Pour consulter l’énoncé, c’est ici
Solution pour le challenge 62
La réponse est non. Pour le voir, considérons la suite définie par :
![]()
![Rendered by QuickLaTeX.com \[y_{n}=\frac{1}{n+1}\sum_{k=0}^{n}\left(-1\right)^{k}\sqrt{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-228feb80375bc03c34e535910337af9b_l3.png)
Alors :
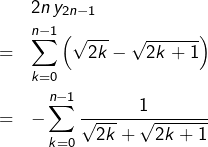
![]()
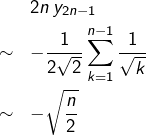
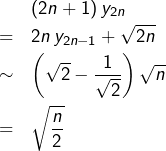
Bref :
![Rendered by QuickLaTeX.com \[\boxed{y_{n}\sim\frac{\left(-1\right)^{n}}{2\sqrt{n}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-646cc2ef8e5137e37cec1b04a54f7451_l3.png)
Pour consulter l’énoncé, c’est ici